
Question Number 187069 by Humble last updated on 13/Feb/23
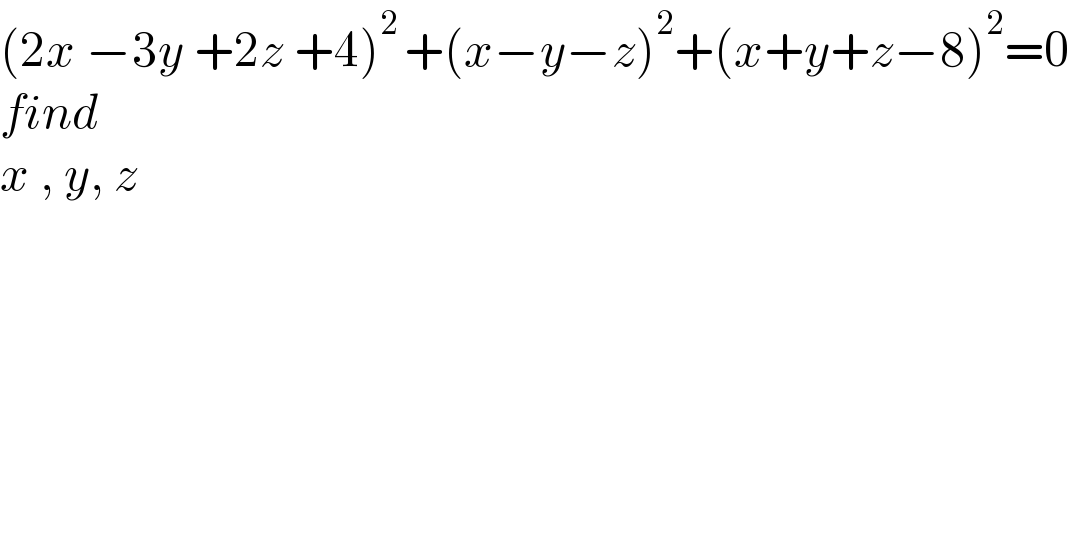
$$\left(\mathrm{2}{x}\:−\mathrm{3}{y}\:+\mathrm{2}{z}\:+\mathrm{4}\right)^{\mathrm{2}\:} +\left({x}−{y}−{z}\right)^{\mathrm{2}} +\left({x}+{y}+{z}−\mathrm{8}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${find} \\ $$$${x}\:,\:{y},\:{z}\: \\ $$
Answered by ARUNG_Brandon_MBU last updated on 13/Feb/23
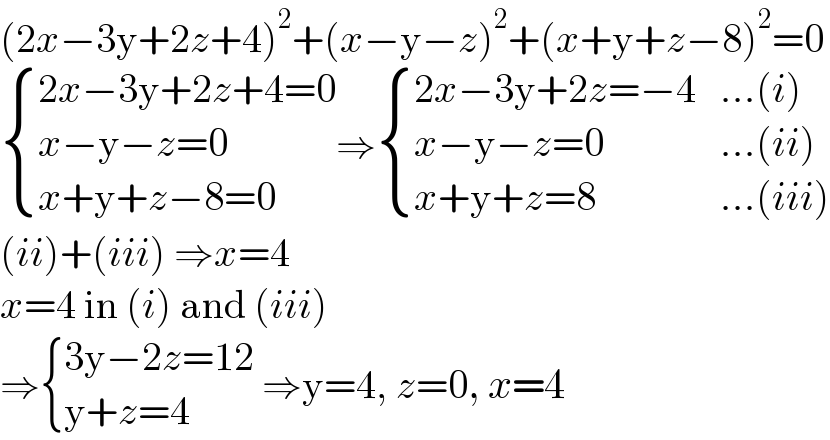
$$\left(\mathrm{2}{x}−\mathrm{3y}+\mathrm{2}{z}+\mathrm{4}\right)^{\mathrm{2}} +\left({x}−\mathrm{y}−{z}\right)^{\mathrm{2}} +\left({x}+\mathrm{y}+{z}−\mathrm{8}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\begin{cases}{\mathrm{2}{x}−\mathrm{3y}+\mathrm{2}{z}+\mathrm{4}=\mathrm{0}}\\{{x}−\mathrm{y}−{z}=\mathrm{0}}\\{{x}+\mathrm{y}+{z}−\mathrm{8}=\mathrm{0}}\end{cases}\Rightarrow\begin{cases}{\mathrm{2}{x}−\mathrm{3y}+\mathrm{2}{z}=−\mathrm{4}}&{...\left({i}\right)}\\{{x}−\mathrm{y}−{z}=\mathrm{0}}&{...\left({ii}\right)}\\{{x}+\mathrm{y}+{z}=\mathrm{8}}&{...\left({iii}\right)}\end{cases} \\ $$$$\left({ii}\right)+\left({iii}\right)\:\Rightarrow{x}=\mathrm{4} \\ $$$${x}=\mathrm{4}\:\mathrm{in}\:\left({i}\right)\:\mathrm{and}\:\left({iii}\right) \\ $$$$\Rightarrow\begin{cases}{\mathrm{3y}−\mathrm{2}{z}=\mathrm{12}}\\{\mathrm{y}+{z}=\mathrm{4}}\end{cases}\:\Rightarrow\mathrm{y}=\mathrm{4},\:{z}=\mathrm{0},\:{x}=\mathrm{4} \\ $$
