
Question Number 186962 by mnjuly1970 last updated on 12/Feb/23
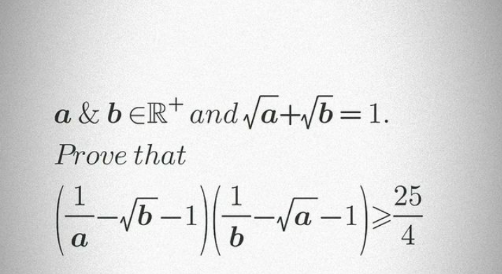
Answered by MJS_new last updated on 12/Feb/23
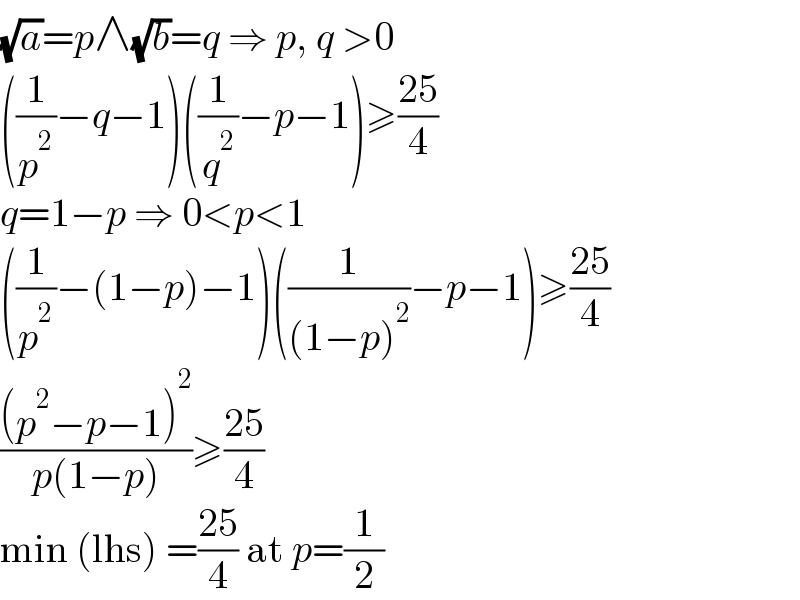
$$\sqrt{{a}}={p}\wedge\sqrt{{b}}={q}\:\Rightarrow\:{p},\:{q}\:>\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{{p}^{\mathrm{2}} }−{q}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{{q}^{\mathrm{2}} }−{p}−\mathrm{1}\right)\geqslant\frac{\mathrm{25}}{\mathrm{4}} \\ $$$${q}=\mathrm{1}−{p}\:\Rightarrow\:\mathrm{0}<{p}<\mathrm{1} \\ $$$$\left(\frac{\mathrm{1}}{{p}^{\mathrm{2}} }−\left(\mathrm{1}−{p}\right)−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\left(\mathrm{1}−{p}\right)^{\mathrm{2}} }−{p}−\mathrm{1}\right)\geqslant\frac{\mathrm{25}}{\mathrm{4}} \\ $$$$\frac{\left({p}^{\mathrm{2}} −{p}−\mathrm{1}\right)^{\mathrm{2}} }{{p}\left(\mathrm{1}−{p}\right)}\geqslant\frac{\mathrm{25}}{\mathrm{4}} \\ $$$$\mathrm{min}\:\left(\mathrm{lhs}\right)\:=\frac{\mathrm{25}}{\mathrm{4}}\:\mathrm{at}\:{p}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
