Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 186952 by Humble last updated on 12/Feb/23

Answered by horsebrand11 last updated on 12/Feb/23

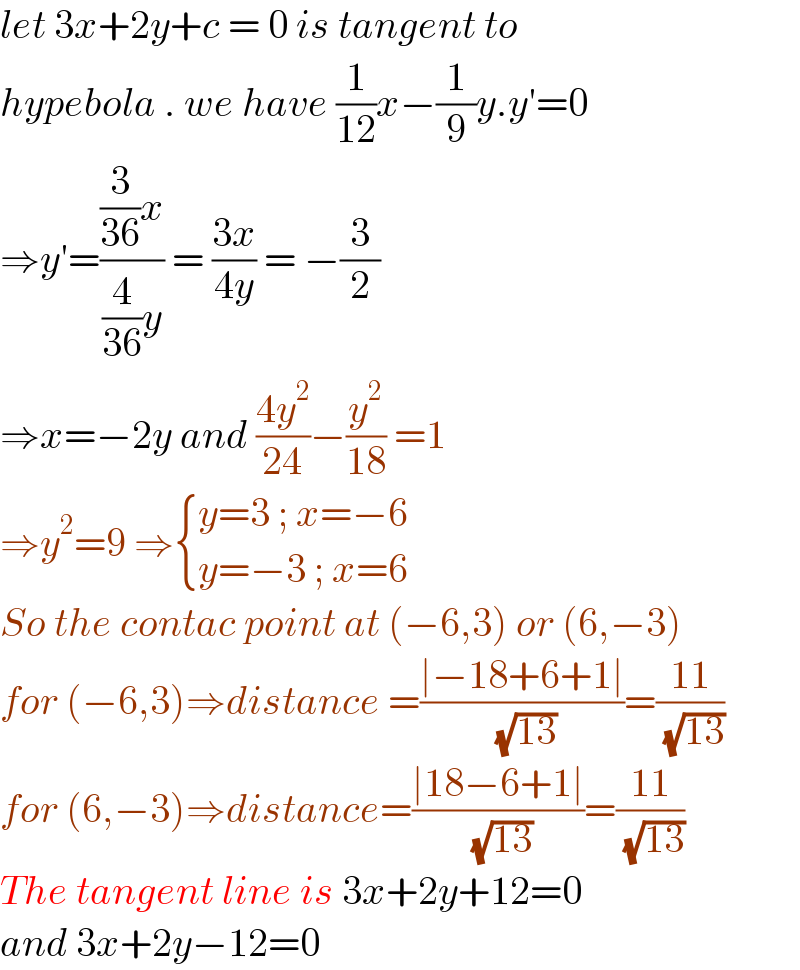
let 3x+2y+c = 0 is tangent to hypebola . we have (1/(12))x−(1/9)y.y′=0 ⇒y′=(((3/(36))x)/((4/(36))y)) = ((3x)/(4y)) = −(3/2) ⇒x=−2y and ((4y^2 )/(24))−(y^2 /(18)) =1 ⇒y^2 =9 ⇒ { ((y=3 ; x=−6)),((y=−3 ; x=6)) :} So the contac point at (−6,3) or (6,−3) for (−6,3)⇒distance =((∣−18+6+1∣)/( (√(13))))=((11)/( (√(13)))) for (6,−3)⇒distance=((∣18−6+1∣)/( (√(13))))=((11)/( (√(13)))) The tangent line is 3x+2y+12=0 and 3x+2y−12=0

$${let}\:\mathrm{3}{x}+\mathrm{2}{y}+{c}\:=\:\mathrm{0}\:{is}\:{tangent}\:{to} \\ $$$${hypebola}\:.\:{we}\:{have}\:\frac{\mathrm{1}}{\mathrm{12}}{x}−\frac{\mathrm{1}}{\mathrm{9}}{y}.{y}'=\mathrm{0} \\ $$$$\Rightarrow{y}'=\frac{\frac{\mathrm{3}}{\mathrm{36}}{x}}{\frac{\mathrm{4}}{\mathrm{36}}{y}}\:=\:\frac{\mathrm{3}{x}}{\mathrm{4}{y}}\:=\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=−\mathrm{2}{y}\:{and}\:\frac{\mathrm{4}{y}^{\mathrm{2}} }{\mathrm{24}}−\frac{{y}^{\mathrm{2}} }{\mathrm{18}}\:=\mathrm{1} \\ $$$$\Rightarrow{y}^{\mathrm{2}} =\mathrm{9}\:\Rightarrow\begin{cases}{{y}=\mathrm{3}\:;\:{x}=−\mathrm{6}}\\{{y}=−\mathrm{3}\:;\:{x}=\mathrm{6}}\end{cases} \\ $$$${So}\:{the}\:{contac}\:{point}\:{at}\:\left(−\mathrm{6},\mathrm{3}\right)\:{or}\:\left(\mathrm{6},−\mathrm{3}\right) \\ $$$${for}\:\left(−\mathrm{6},\mathrm{3}\right)\Rightarrow{distance}\:=\frac{\mid−\mathrm{18}+\mathrm{6}+\mathrm{1}\mid}{\:\sqrt{\mathrm{13}}}=\frac{\mathrm{11}}{\:\sqrt{\mathrm{13}}} \\ $$$${for}\:\left(\mathrm{6},−\mathrm{3}\right)\Rightarrow{distance}=\frac{\mid\mathrm{18}−\mathrm{6}+\mathrm{1}\mid}{\:\sqrt{\mathrm{13}}}=\frac{\mathrm{11}}{\:\sqrt{\mathrm{13}}} \\ $$$${The}\:{tangent}\:{line}\:{is}\:\mathrm{3}{x}+\mathrm{2}{y}+\mathrm{12}=\mathrm{0} \\ $$$${and}\:\mathrm{3}{x}+\mathrm{2}{y}−\mathrm{12}=\mathrm{0}\: \\ $$

Commented by horsebrand11 last updated on 12/Feb/23

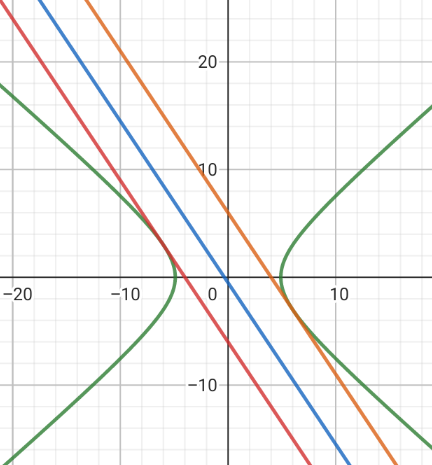
Commented by Humble last updated on 12/Feb/23

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by mr W last updated on 12/Feb/23

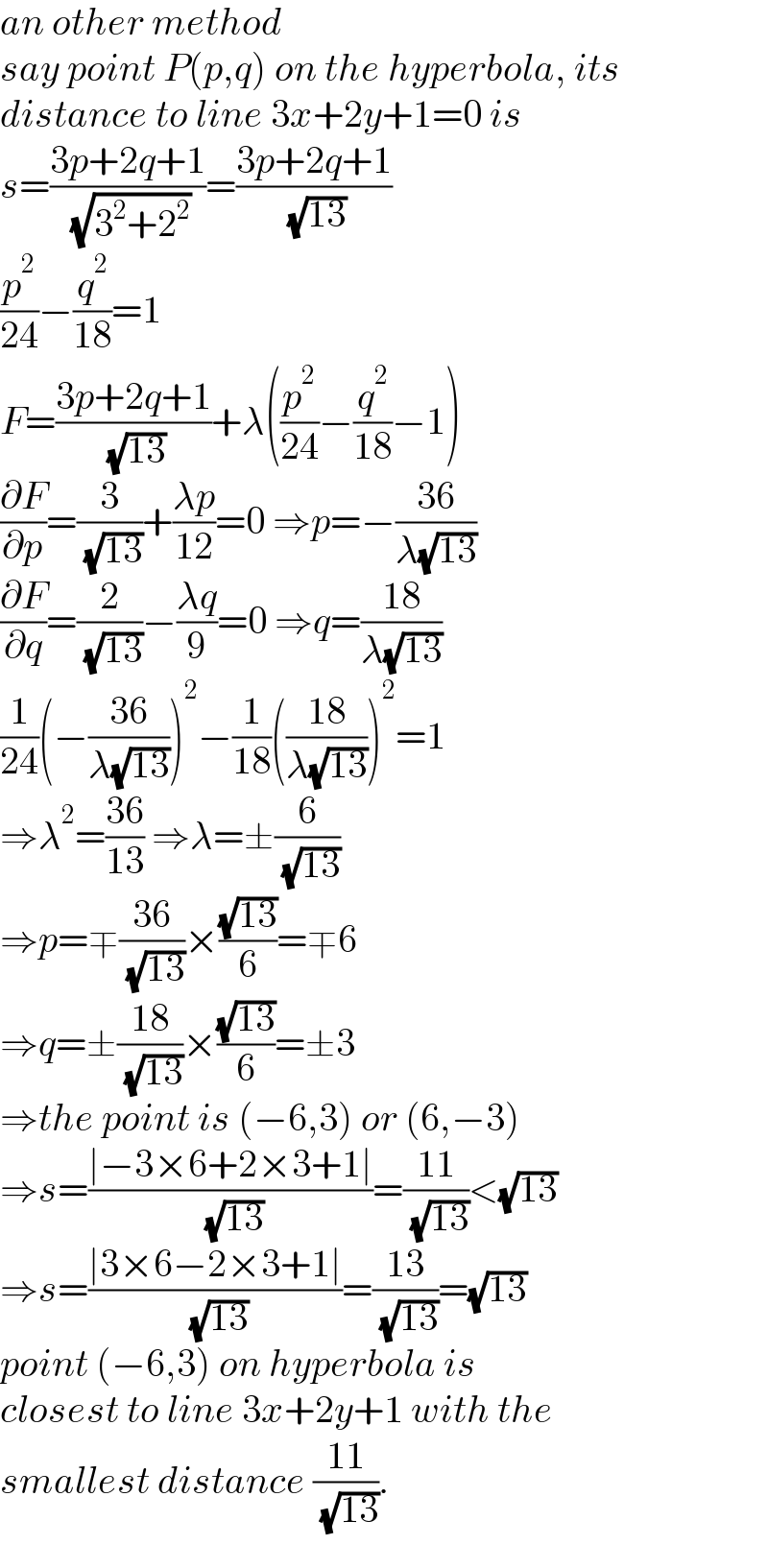
an other method say point P(p,q) on the hyperbola, its distance to line 3x+2y+1=0 is s=((3p+2q+1)/( (√(3^2 +2^2 ))))=((3p+2q+1)/( (√(13)))) (p^2 /(24))−(q^2 /(18))=1 F=((3p+2q+1)/( (√(13))))+λ((p^2 /(24))−(q^2 /(18))−1) (∂F/∂p)=(3/( (√(13))))+((λp)/(12))=0 ⇒p=−((36)/(λ(√(13)))) (∂F/∂q)=(2/( (√(13))))−((λq)/9)=0 ⇒q=((18)/(λ(√(13)))) (1/(24))(−((36)/(λ(√(13)))))^2 −(1/(18))(((18)/(λ(√(13)))))^2 =1 ⇒λ^2 =((36)/(13)) ⇒λ=±(6/( (√(13)))) ⇒p=∓((36)/( (√(13))))×((√(13))/6)=∓6 ⇒q=±((18)/( (√(13))))×((√(13))/6)=±3 ⇒the point is (−6,3) or (6,−3) ⇒s=((∣−3×6+2×3+1∣)/( (√(13))))=((11)/( (√(13))))<(√(13)) ⇒s=((∣3×6−2×3+1∣)/( (√(13))))=((13)/( (√(13))))=(√(13)) point (−6,3) on hyperbola is closest to line 3x+2y+1 with the smallest distance ((11)/( (√(13)))).

$${an}\:{other}\:{method} \\ $$$${say}\:{point}\:{P}\left({p},{q}\right)\:{on}\:{the}\:{hyperbola},\:{its} \\ $$$${distance}\:{to}\:{line}\:\mathrm{3}{x}+\mathrm{2}{y}+\mathrm{1}=\mathrm{0}\:{is} \\ $$$${s}=\frac{\mathrm{3}{p}+\mathrm{2}{q}+\mathrm{1}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}=\frac{\mathrm{3}{p}+\mathrm{2}{q}+\mathrm{1}}{\:\sqrt{\mathrm{13}}} \\ $$$$\frac{{p}^{\mathrm{2}} }{\mathrm{24}}−\frac{{q}^{\mathrm{2}} }{\mathrm{18}}=\mathrm{1} \\ $$$${F}=\frac{\mathrm{3}{p}+\mathrm{2}{q}+\mathrm{1}}{\:\sqrt{\mathrm{13}}}+\lambda\left(\frac{{p}^{\mathrm{2}} }{\mathrm{24}}−\frac{{q}^{\mathrm{2}} }{\mathrm{18}}−\mathrm{1}\right) \\ $$$$\frac{\partial{F}}{\partial{p}}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}}+\frac{\lambda{p}}{\mathrm{12}}=\mathrm{0}\:\Rightarrow{p}=−\frac{\mathrm{36}}{\lambda\sqrt{\mathrm{13}}} \\ $$$$\frac{\partial{F}}{\partial{q}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}−\frac{\lambda{q}}{\mathrm{9}}=\mathrm{0}\:\Rightarrow{q}=\frac{\mathrm{18}}{\lambda\sqrt{\mathrm{13}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{24}}\left(−\frac{\mathrm{36}}{\lambda\sqrt{\mathrm{13}}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{18}}\left(\frac{\mathrm{18}}{\lambda\sqrt{\mathrm{13}}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} =\frac{\mathrm{36}}{\mathrm{13}}\:\Rightarrow\lambda=\pm\frac{\mathrm{6}}{\:\sqrt{\mathrm{13}}} \\ $$$$\Rightarrow{p}=\mp\frac{\mathrm{36}}{\:\sqrt{\mathrm{13}}}×\frac{\sqrt{\mathrm{13}}}{\mathrm{6}}=\mp\mathrm{6} \\ $$$$\Rightarrow{q}=\pm\frac{\mathrm{18}}{\:\sqrt{\mathrm{13}}}×\frac{\sqrt{\mathrm{13}}}{\mathrm{6}}=\pm\mathrm{3} \\ $$$$\Rightarrow{the}\:{point}\:{is}\:\left(−\mathrm{6},\mathrm{3}\right)\:{or}\:\left(\mathrm{6},−\mathrm{3}\right) \\ $$$$\Rightarrow{s}=\frac{\mid−\mathrm{3}×\mathrm{6}+\mathrm{2}×\mathrm{3}+\mathrm{1}\mid}{\:\sqrt{\mathrm{13}}}=\frac{\mathrm{11}}{\:\sqrt{\mathrm{13}}}<\sqrt{\mathrm{13}} \\ $$$$\Rightarrow{s}=\frac{\mid\mathrm{3}×\mathrm{6}−\mathrm{2}×\mathrm{3}+\mathrm{1}\mid}{\:\sqrt{\mathrm{13}}}=\frac{\mathrm{13}}{\:\sqrt{\mathrm{13}}}=\sqrt{\mathrm{13}} \\ $$$${point}\:\left(−\mathrm{6},\mathrm{3}\right)\:{on}\:{hyperbola}\:{is} \\ $$$${closest}\:{to}\:{line}\:\mathrm{3}{x}+\mathrm{2}{y}+\mathrm{1}\:{with}\:{the} \\ $$$${smallest}\:{distance}\:\frac{\mathrm{11}}{\:\sqrt{\mathrm{13}}}. \\ $$

Commented by mr W last updated on 12/Feb/23

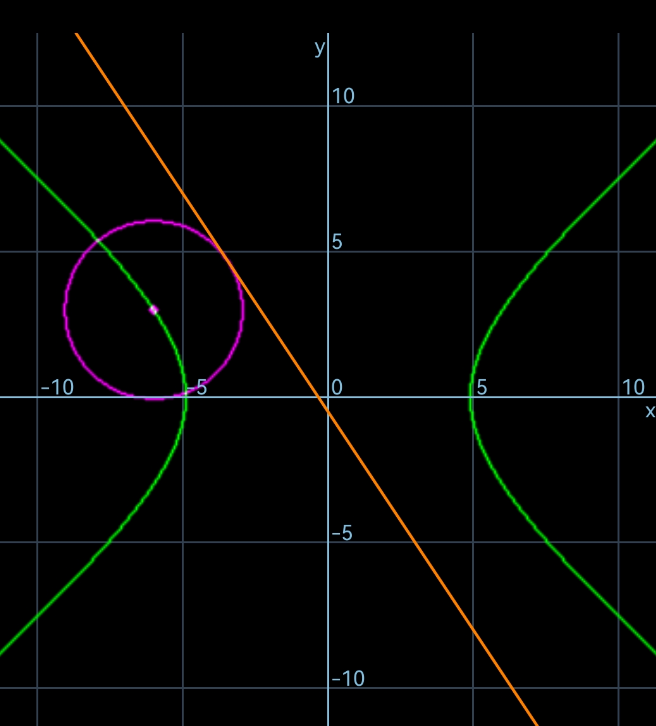
Commented by Humble last updated on 12/Feb/23

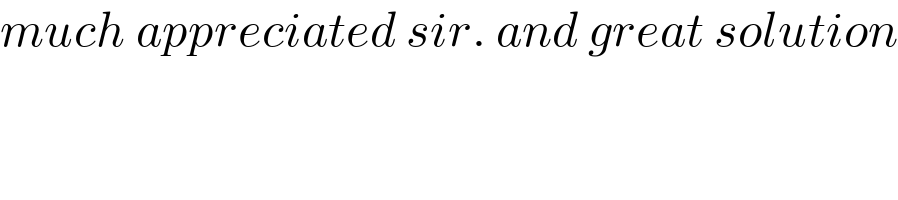
much appreciated sir. and great solution

$${much}\:{appreciated}\:{sir}.\:{and}\:{great}\:{solution} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com