Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 186926 by cortano12 last updated on 12/Feb/23

Commented by cortano12 last updated on 12/Feb/23

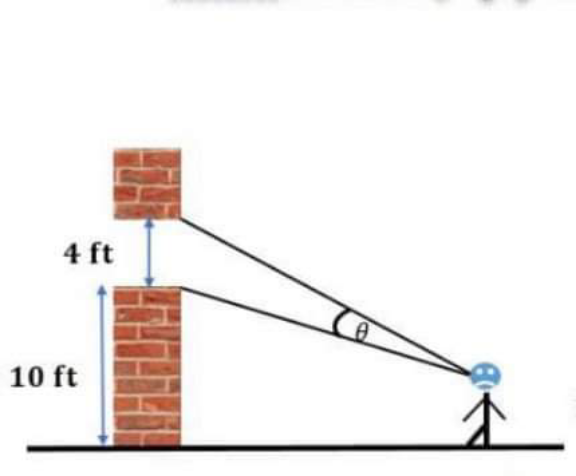
Q2 A 6ft tall man is moving at a speed of 2ft/s towards a building with a window whose base is 10ft above the ground and the height of the window is 4ft. If the angle between the lines of the man’s gaze is up and down the window, find the rate of change of the angle when the man is 16ft away from the base of the building

Answered by manxsol last updated on 12/Feb/23

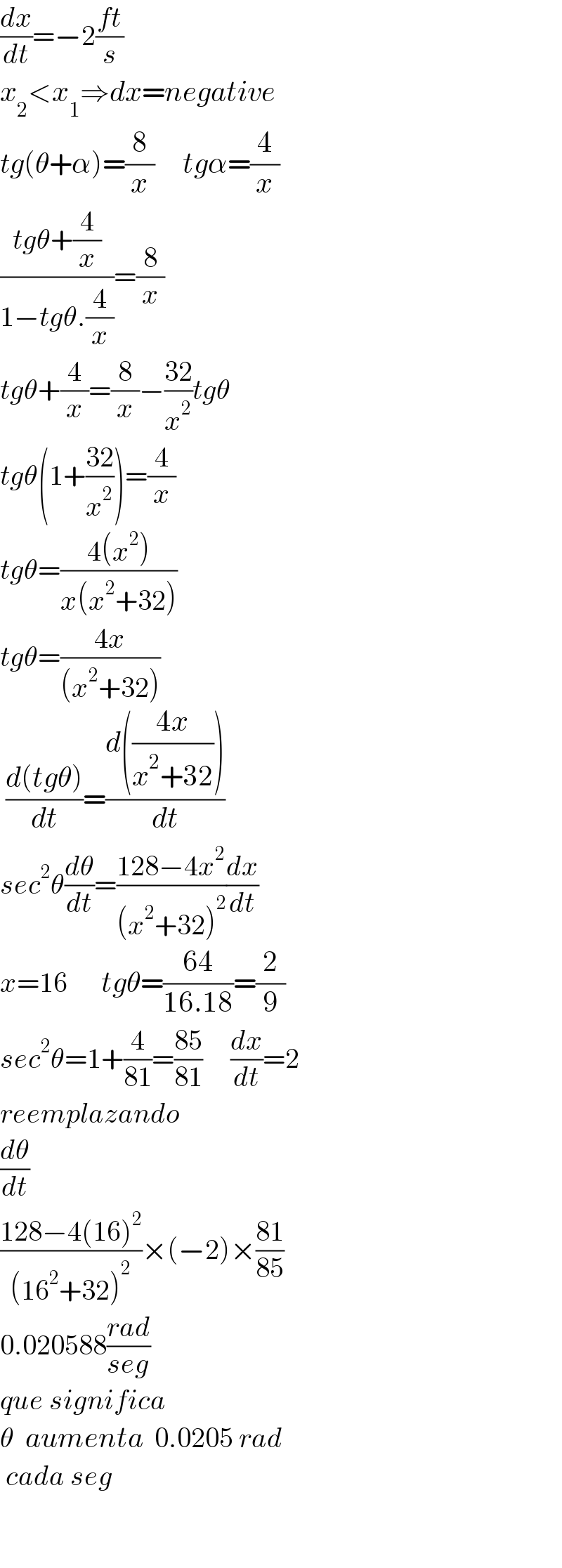
(dx/dt)=−2((ft)/s) x_2 <x_1 ⇒dx=negative tg(θ+α)=(8/x) tgα=(4/x) ((tgθ+(4/x))/(1−tgθ.(4/x)))=(8/x) tgθ+(4/x)=(8/x)−((32)/x^2 )tgθ tgθ(1+((32)/x^2 ))=(4/x) tgθ=((4(x^2 ))/(x(x^2 +32))) tgθ=((4x)/((x^2 +32))) ((d(tgθ))/dt)=((d(((4x)/(x^2 +32))))/dt) sec^2 θ(dθ/dt)=((128−4x^2 )/((x^2 +32)^2 ))(dx/dt) x=16 tgθ=((64)/(16.18))=(2/9) sec^2 θ=1+(4/(81))=((85)/(81)) (dx/dt)=2 reemplazando (dθ/dt) ((128−4(16)^2 )/((16^2 +32)^2 ))×(−2)×((81)/(85)) 0.020588((rad)/(seg)) que significa θ aumenta 0.0205 rad cada seg

$$\frac{{dx}}{{dt}}=−\mathrm{2}\frac{{ft}}{{s}}\:\:\:\:\:\:\: \\ $$$${x}_{\mathrm{2}} <{x}_{\mathrm{1}} \Rightarrow{dx}={negative} \\ $$$${tg}\left(\theta+\alpha\right)=\frac{\mathrm{8}}{{x}}\:\:\:\:\:{tg}\alpha=\frac{\mathrm{4}}{{x}} \\ $$$$\frac{{tg}\theta+\frac{\mathrm{4}}{{x}}}{\mathrm{1}−{tg}\theta.\frac{\mathrm{4}}{{x}}}=\frac{\mathrm{8}}{{x}} \\ $$$${tg}\theta+\frac{\mathrm{4}}{{x}}=\frac{\mathrm{8}}{{x}}−\frac{\mathrm{32}}{{x}^{\mathrm{2}} }{tg}\theta \\ $$$${tg}\theta\left(\mathrm{1}+\frac{\mathrm{32}}{{x}^{\mathrm{2}} }\right)=\frac{\mathrm{4}}{{x}} \\ $$$${tg}\theta=\frac{\mathrm{4}\left({x}^{\mathrm{2}} \right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{32}\right)} \\ $$$${tg}\theta=\frac{\mathrm{4}{x}}{\left({x}^{\mathrm{2}} +\mathrm{32}\right)} \\ $$$$\:\frac{{d}\left({tg}\theta\right)}{{dt}}=\frac{{d}\left(\frac{\mathrm{4}{x}}{{x}^{\mathrm{2}} +\mathrm{32}}\right)}{{dt}} \\ $$$${sec}^{\mathrm{2}} \theta\frac{{d}\theta}{{dt}}=\frac{\mathrm{128}−\mathrm{4}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{32}\right)^{\mathrm{2}} }\frac{{dx}}{{dt}} \\ $$$${x}=\mathrm{16}\:\:\:\:\:\:{tg}\theta=\frac{\mathrm{64}}{\mathrm{16}.\mathrm{18}}=\frac{\mathrm{2}}{\mathrm{9}} \\ $$$${sec}^{\mathrm{2}} \theta=\mathrm{1}+\frac{\mathrm{4}}{\mathrm{81}}=\frac{\mathrm{85}}{\mathrm{81}}\:\:\:\:\:\frac{{dx}}{{dt}}=\mathrm{2} \\ $$$${reemplazando} \\ $$$$\frac{{d}\theta}{{dt}} \\ $$$$\frac{\mathrm{128}−\mathrm{4}\left(\mathrm{16}\right)^{\mathrm{2}} }{\left(\mathrm{16}^{\mathrm{2}} +\mathrm{32}\right)^{\mathrm{2}} }×\left(−\mathrm{2}\right)×\frac{\mathrm{81}}{\mathrm{85}} \\ $$$$\mathrm{0}.\mathrm{020588}\frac{{rad}}{{seg}} \\ $$$${que}\:{significa} \\ $$$$\theta\:\:{aumenta}\:\:\mathrm{0}.\mathrm{0205}\:{rad} \\ $$$$\:{cada}\:{seg} \\ $$$$ \\ $$$$ \\ $$

Commented by mr W last updated on 13/Feb/23

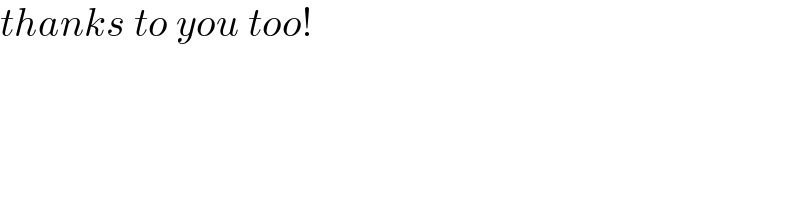
thanks to you too!

$${thanks}\:{to}\:{you}\:{too}! \\ $$

Commented by manxsol last updated on 12/Feb/23

It must be by the combination of the graphic with the text= I will correct it.Listo corregido .Gracias sir W

$${It}\:{must}\:{be}\:{by}\:{the}\:{combination} \\ $$$$\:{of}\:{the}\:{graphic}\:{with}\:{the}\:{text}= \\ $$$${I}\:{will}\:{correct}\:{it}.{Listo}\:{corregido} \\ $$$$.{Gracias}\:{sir}\:{W} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com