Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 18653 by Tinkutara last updated on 26/Jul/17

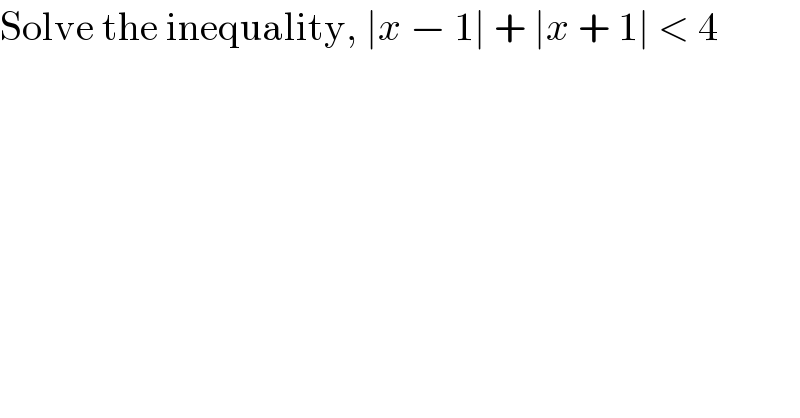
Solve the inequality, ∣x − 1∣ + ∣x + 1∣ < 4

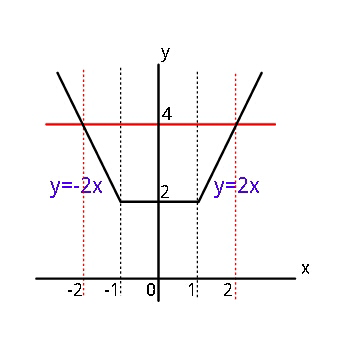
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{inequality},\:\mid{x}\:−\:\mathrm{1}\mid\:+\:\mid{x}\:+\:\mathrm{1}\mid\:<\:\mathrm{4} \\ $$

Answered by ajfour last updated on 26/Jul/17

If x<−1 −(x−1)−(x+1)<4 ⇒ 2x>−4 or x> −2 hence x∈(−2 ,−1) If −1≤x<1 −(x−1)+x+1<4 ⇒ 2<4 so x∈[−1,1) If 1≤x x−1+x+1<4 ⇒ 2x<4 or x<2 x∈[1,2) Taking union of the three cases, x∈(−2,2) .

$$\mathrm{If}\:\mathrm{x}<−\mathrm{1} \\ $$ $$−\left(\mathrm{x}−\mathrm{1}\right)−\left(\mathrm{x}+\mathrm{1}\right)<\mathrm{4} \\ $$ $$\Rightarrow\:\mathrm{2x}>−\mathrm{4}\:\:\mathrm{or}\:\:\mathrm{x}>\:−\mathrm{2} \\ $$ $$\mathrm{hence}\:\mathrm{x}\in\left(−\mathrm{2}\:,−\mathrm{1}\right) \\ $$ $$\mathrm{If}\:−\mathrm{1}\leqslant\mathrm{x}<\mathrm{1} \\ $$ $$−\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{x}+\mathrm{1}<\mathrm{4} \\ $$ $$\Rightarrow\:\mathrm{2}<\mathrm{4}\: \\ $$ $$\mathrm{so}\:\:\mathrm{x}\in\left[−\mathrm{1},\mathrm{1}\right) \\ $$ $$\mathrm{If}\:\mathrm{1}\leqslant\mathrm{x} \\ $$ $$\mathrm{x}−\mathrm{1}+\mathrm{x}+\mathrm{1}<\mathrm{4} \\ $$ $$\Rightarrow\:\mathrm{2x}<\mathrm{4}\:\:\mathrm{or}\:\:\:\mathrm{x}<\mathrm{2} \\ $$ $$\:\:\mathrm{x}\in\left[\mathrm{1},\mathrm{2}\right) \\ $$ $$\mathrm{Taking}\:\mathrm{union}\:\mathrm{of}\:\mathrm{the}\:\mathrm{three}\:\mathrm{cases}, \\ $$ $$\:\:\:\:\:\mathrm{x}\in\left(−\mathrm{2},\mathrm{2}\right)\:. \\ $$

Commented byTinkutara last updated on 26/Jul/17

Thank you very much ajfour Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{ajfour}\:\mathrm{Sir}! \\ $$

Commented byajfour last updated on 26/Jul/17

Terms of Service

Privacy Policy

Contact: info@tinkutara.com