
Question Number 186053 by Rupesh123 last updated on 31/Jan/23
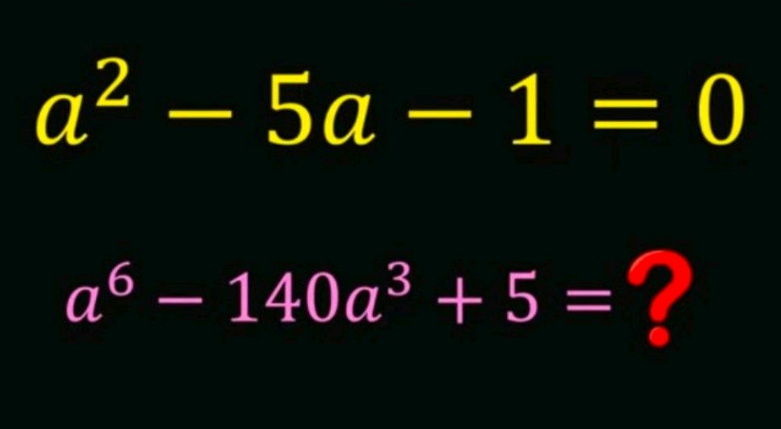
Answered by SEKRET last updated on 31/Jan/23
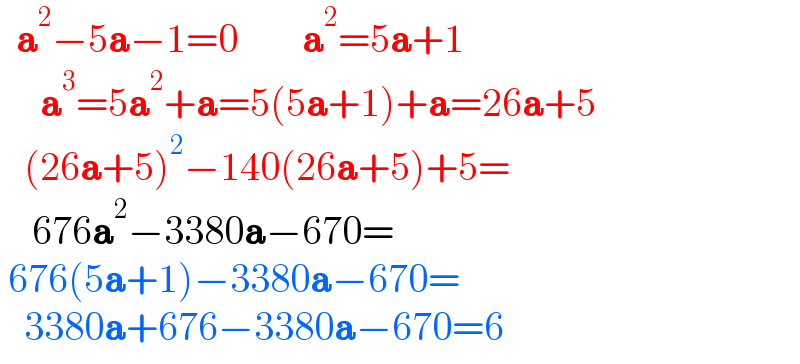
$$\:\:\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{\mathrm{a}}−\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{a}}^{\mathrm{2}} =\mathrm{5}\boldsymbol{\mathrm{a}}+\mathrm{1} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{a}}^{\mathrm{3}} =\mathrm{5}\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{a}}=\mathrm{5}\left(\mathrm{5}\boldsymbol{\mathrm{a}}+\mathrm{1}\right)+\boldsymbol{\mathrm{a}}=\mathrm{26}\boldsymbol{\mathrm{a}}+\mathrm{5} \\ $$$$\:\:\:\left(\mathrm{26}\boldsymbol{\mathrm{a}}+\mathrm{5}\right)^{\mathrm{2}} −\mathrm{140}\left(\mathrm{26}\boldsymbol{\mathrm{a}}+\mathrm{5}\right)+\mathrm{5}= \\ $$$$\:\:\:\:\mathrm{676}\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{3380}\boldsymbol{\mathrm{a}}−\mathrm{670}= \\ $$$$\:\mathrm{676}\left(\mathrm{5}\boldsymbol{\mathrm{a}}+\mathrm{1}\right)−\mathrm{3380}\boldsymbol{\mathrm{a}}−\mathrm{670}= \\ $$$$\:\:\:\mathrm{3380}\boldsymbol{\mathrm{a}}+\mathrm{676}−\mathrm{3380}\boldsymbol{\mathrm{a}}−\mathrm{670}=\mathrm{6}\: \\ $$
Answered by Rasheed.Sindhi last updated on 31/Jan/23
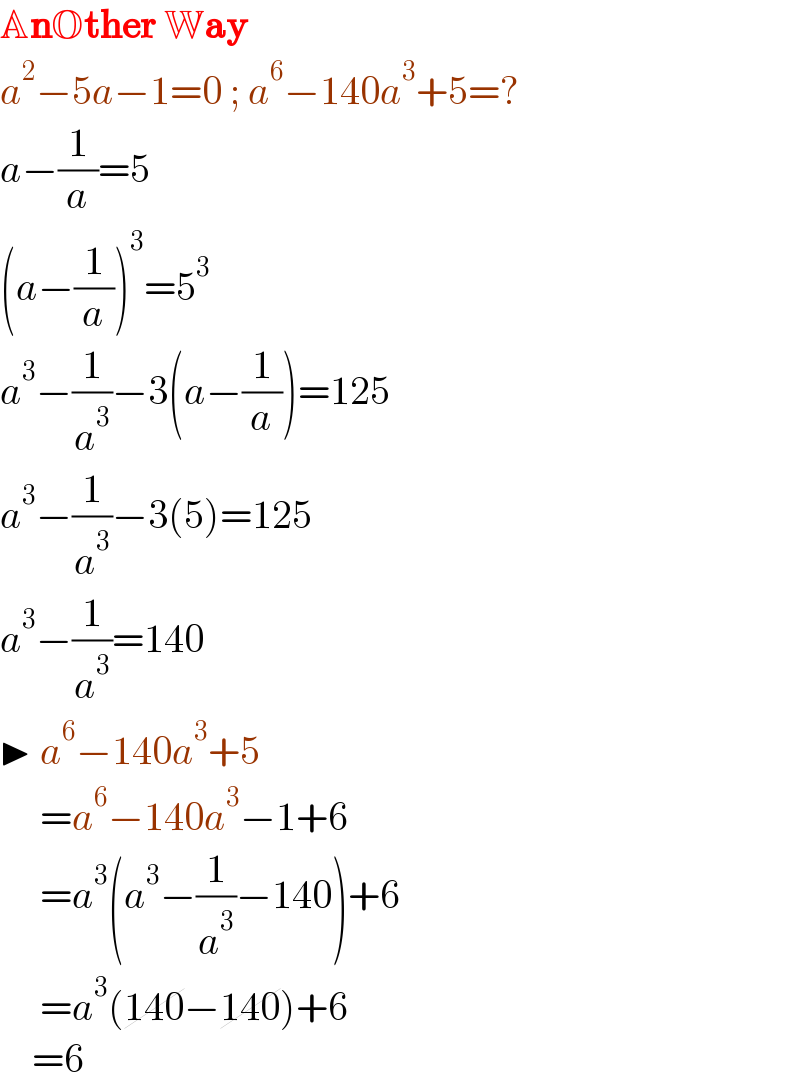
$$\mathbb{A}\boldsymbol{\mathrm{n}}\mathbb{O}\boldsymbol{\mathrm{ther}}\:\mathbb{W}\boldsymbol{\mathrm{ay}} \\ $$$${a}^{\mathrm{2}} −\mathrm{5}{a}−\mathrm{1}=\mathrm{0}\:;\:{a}^{\mathrm{6}} −\mathrm{140}{a}^{\mathrm{3}} +\mathrm{5}=? \\ $$$${a}−\frac{\mathrm{1}}{{a}}=\mathrm{5}\: \\ $$$$\left({a}−\frac{\mathrm{1}}{{a}}\right)^{\mathrm{3}} =\mathrm{5}^{\mathrm{3}} \\ $$$${a}^{\mathrm{3}} −\frac{\mathrm{1}}{{a}^{\mathrm{3}} }−\mathrm{3}\left({a}−\frac{\mathrm{1}}{{a}}\right)=\mathrm{125} \\ $$$${a}^{\mathrm{3}} −\frac{\mathrm{1}}{{a}^{\mathrm{3}} }−\mathrm{3}\left(\mathrm{5}\right)=\mathrm{125} \\ $$$${a}^{\mathrm{3}} −\frac{\mathrm{1}}{{a}^{\mathrm{3}} }=\mathrm{140} \\ $$$$\blacktriangleright\:{a}^{\mathrm{6}} −\mathrm{140}{a}^{\mathrm{3}} +\mathrm{5} \\ $$$$\:\:\:\:\:={a}^{\mathrm{6}} −\mathrm{140}{a}^{\mathrm{3}} −\mathrm{1}+\mathrm{6} \\ $$$$\:\:\:\:\:={a}^{\mathrm{3}} \left({a}^{\mathrm{3}} −\frac{\mathrm{1}}{{a}^{\mathrm{3}} }−\mathrm{140}\right)+\mathrm{6} \\ $$$$\:\:\:\:\:={a}^{\mathrm{3}} \left(\cancel{\mathrm{140}}−\cancel{\mathrm{140}}\right)+\mathrm{6} \\ $$$$\:\:\:\:=\mathrm{6} \\ $$
