
Question Number 185372 by Mingma last updated on 20/Jan/23
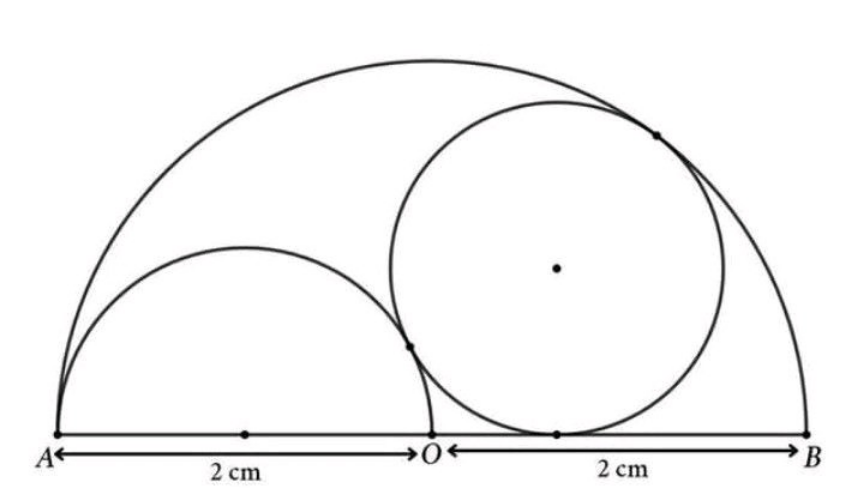
Answered by a.lgnaoui last updated on 21/Jan/23
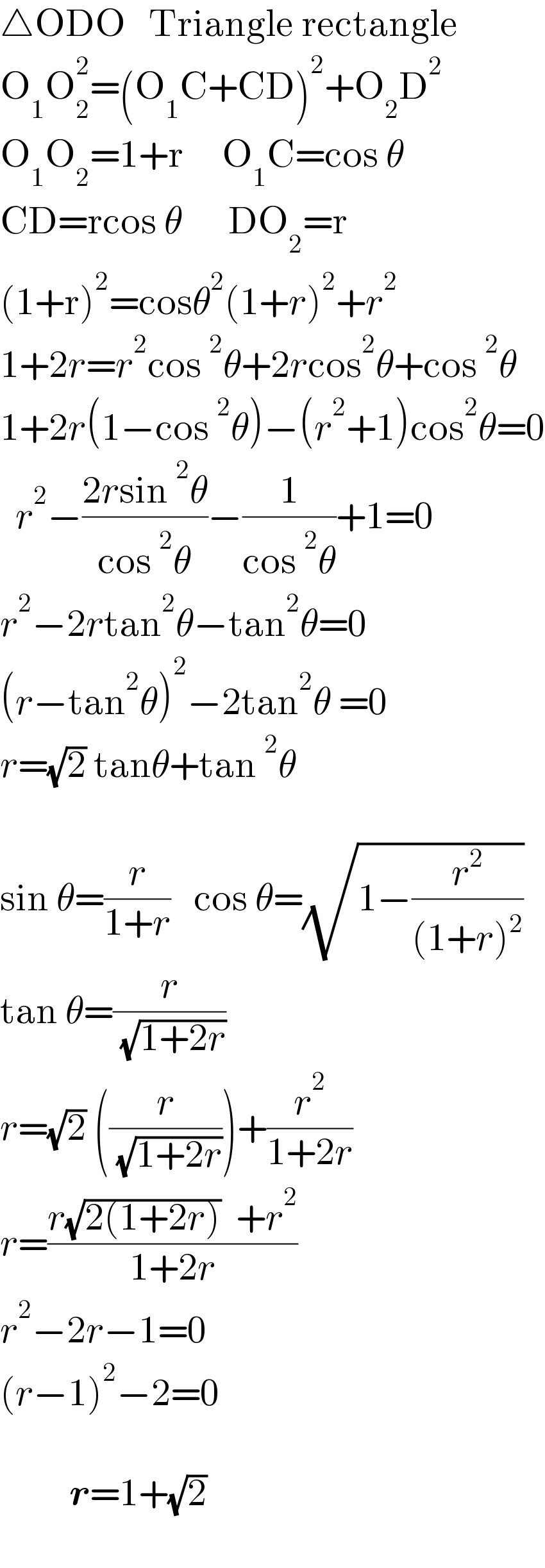
$$\bigtriangleup\mathrm{ODO}\:\:\:\mathrm{Triangle}\:\mathrm{rectangle} \\ $$$$\mathrm{O}_{\mathrm{1}} \mathrm{O}_{\mathrm{2}} ^{\mathrm{2}} =\left(\mathrm{O}_{\mathrm{1}} \mathrm{C}+\mathrm{CD}\right)^{\mathrm{2}} +\mathrm{O}_{\mathrm{2}} \mathrm{D}^{\mathrm{2}} \\ $$$$\mathrm{O}_{\mathrm{1}} \mathrm{O}_{\mathrm{2}} =\mathrm{1}+\mathrm{r}\:\:\:\:\:\mathrm{O}_{\mathrm{1}} \mathrm{C}=\mathrm{cos}\:\theta \\ $$$$\mathrm{CD}=\mathrm{rcos}\:\theta\:\:\:\:\:\:\mathrm{DO}_{\mathrm{2}} =\mathrm{r} \\ $$$$\left(\mathrm{1}+\mathrm{r}\right)^{\mathrm{2}} =\mathrm{cos}\theta^{\mathrm{2}} \left(\mathrm{1}+{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{2}{r}={r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{2}{r}\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\mathrm{1}+\mathrm{2}{r}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)−\left({r}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{cos}^{\mathrm{2}} \theta=\mathrm{0} \\ $$$$\:\:{r}^{\mathrm{2}} −\frac{\mathrm{2}{r}\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{cos}\:^{\mathrm{2}} \theta}−\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \theta}+\mathrm{1}=\mathrm{0} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{r}\mathrm{tan}^{\mathrm{2}} \theta−\mathrm{tan}^{\mathrm{2}} \theta=\mathrm{0}\: \\ $$$$\left({r}−\mathrm{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} −\mathrm{2tan}^{\mathrm{2}} \theta\:=\mathrm{0} \\ $$$${r}=\sqrt{\mathrm{2}}\:\mathrm{tan}\theta+\mathrm{tan}\:^{\mathrm{2}} \theta\: \\ $$$$\: \\ $$$$\mathrm{sin}\:\theta=\frac{{r}}{\mathrm{1}+{r}}\:\:\:\mathrm{cos}\:\theta=\sqrt{\mathrm{1}−\frac{{r}^{\mathrm{2}} }{\left(\mathrm{1}+{r}\right)^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\theta=\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{2}{r}}} \\ $$$${r}=\sqrt{\mathrm{2}}\:\left(\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{2}{r}}}\right)+\frac{{r}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}{r}} \\ $$$${r}=\frac{{r}\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{2}{r}\right)}\:\:+{r}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}{r}} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{r}−\mathrm{1}=\mathrm{0} \\ $$$$\left({r}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{0} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{r}}=\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$ \\ $$
Commented by mr W last updated on 21/Jan/23

$${totally}\:{wrong}! \\ $$$${it}'{s}\:{clear}\:{r}<\mathrm{1}. \\ $$
Commented by a.lgnaoui last updated on 21/Jan/23
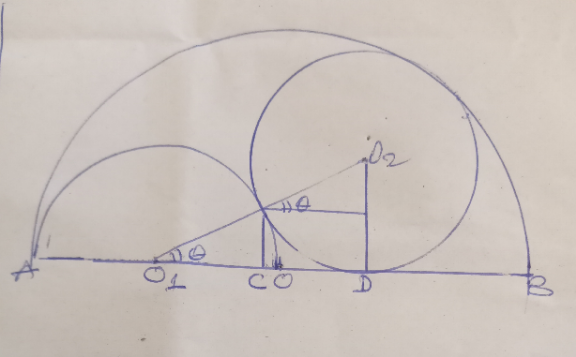
Answered by mr W last updated on 21/Jan/23
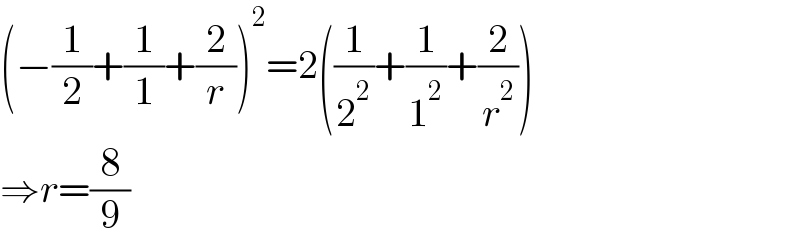
$$\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{2}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{2}}{{r}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{r}=\frac{\mathrm{8}}{\mathrm{9}} \\ $$
