
Question Number 184774 by lapache last updated on 11/Jan/23
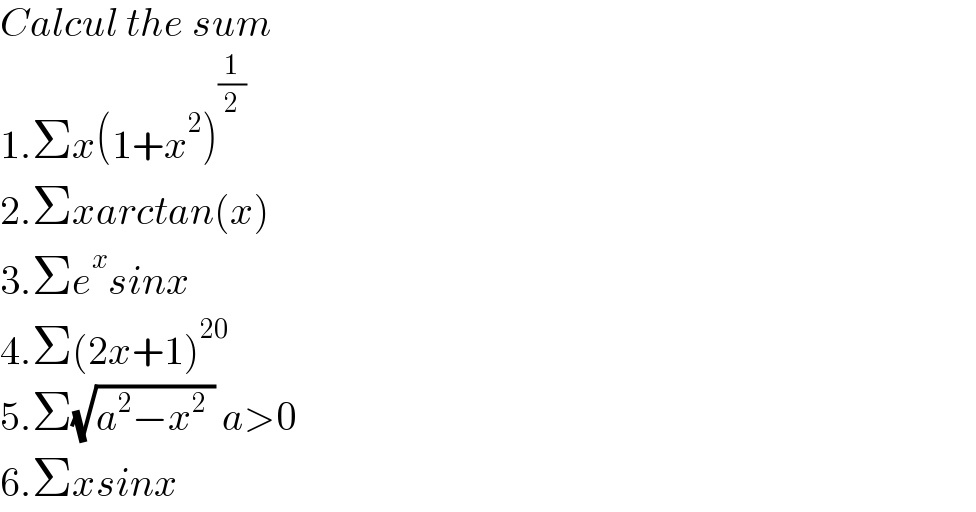
$${Calcul}\:{the}\:{sum} \\ $$ $$\mathrm{1}.\Sigma{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$ $$\mathrm{2}.\Sigma{xarctan}\left({x}\right) \\ $$ $$\mathrm{3}.\Sigma{e}^{{x}} {sinx} \\ $$ $$\mathrm{4}.\Sigma\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{20}} \\ $$ $$\mathrm{5}.\Sigma\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} \:}\:{a}>\mathrm{0} \\ $$ $$\mathrm{6}.\Sigma{xsinx} \\ $$
Commented bymr W last updated on 11/Jan/23

$$\Sigma{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:{makes}\:\:{no}\:{sense},\:{the}\:{other}\: \\ $$ $${ones}\:{also}. \\ $$ $${please}\:{study}\:{at}\:{first}\:{what}\:\Sigma\:{means} \\ $$ $${and}\:{how}\:{to}\:{use}\:{it}\:{and}\:{then}\:{check}\:{your} \\ $$ $${question}\:{again}. \\ $$ $$\underset{{x}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}{x}^{\mathrm{2}} \:{makes}\:{sense}. \\ $$ $$\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}{x}^{\mathrm{2}} \:{makes}\:{also}\:{sense}. \\ $$ $$\int_{\mathrm{1}} ^{\mathrm{100}} {x}^{\mathrm{2}} {dx}\:{makes}\:{sense}. \\ $$ $$\int{x}^{\mathrm{2}} {dx}\:{makes}\:{also}\:{sense}. \\ $$ $$... \\ $$
Commented bySEKRET last updated on 11/Jan/23

$$ \\ $$ 👍👍👍\\n
Answered by SEKRET last updated on 11/Jan/23

$$\:\infty;\propto;\propto;\propto;\infty;\infty \\ $$ $$ \\ $$
