
Question Number 18448 by ankit kumar sharma last updated on 21/Jul/17
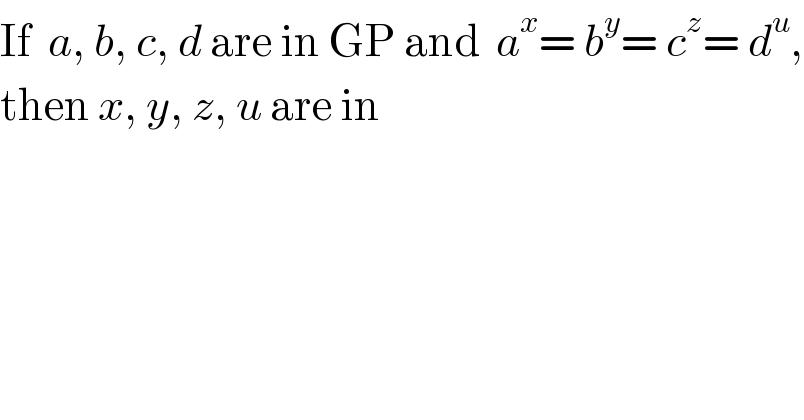
$$\mathrm{If}\:\:{a},\:{b},\:{c},\:{d}\:\mathrm{are}\:\mathrm{in}\:\mathrm{GP}\:\mathrm{and}\:\:{a}^{{x}} =\:{b}^{{y}} =\:{c}^{{z}} =\:{d}^{{u}} , \\ $$$$\mathrm{then}\:{x},\:{y},\:{z},\:{u}\:\mathrm{are}\:\mathrm{in} \\ $$
Answered by Tinkutara last updated on 21/Jul/17
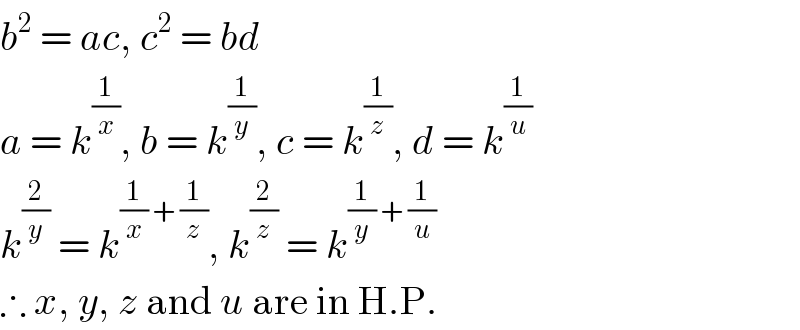
$${b}^{\mathrm{2}} \:=\:{ac},\:{c}^{\mathrm{2}} \:=\:{bd} \\ $$$${a}\:=\:{k}^{\frac{\mathrm{1}}{{x}}} ,\:{b}\:=\:{k}^{\frac{\mathrm{1}}{{y}}} ,\:{c}\:=\:{k}^{\frac{\mathrm{1}}{{z}}} ,\:{d}\:=\:{k}^{\frac{\mathrm{1}}{{u}}} \\ $$$${k}^{\frac{\mathrm{2}}{{y}}} \:=\:{k}^{\frac{\mathrm{1}}{{x}}\:+\:\frac{\mathrm{1}}{{z}}} ,\:{k}^{\frac{\mathrm{2}}{{z}}} \:=\:{k}^{\frac{\mathrm{1}}{{y}}\:+\:\frac{\mathrm{1}}{{u}}} \\ $$$$\therefore\:{x},\:{y},\:{z}\:\mathrm{and}\:{u}\:\mathrm{are}\:\mathrm{in}\:\mathrm{H}.\mathrm{P}. \\ $$
