
Question Number 1844 by 123456 last updated on 12/Oct/15
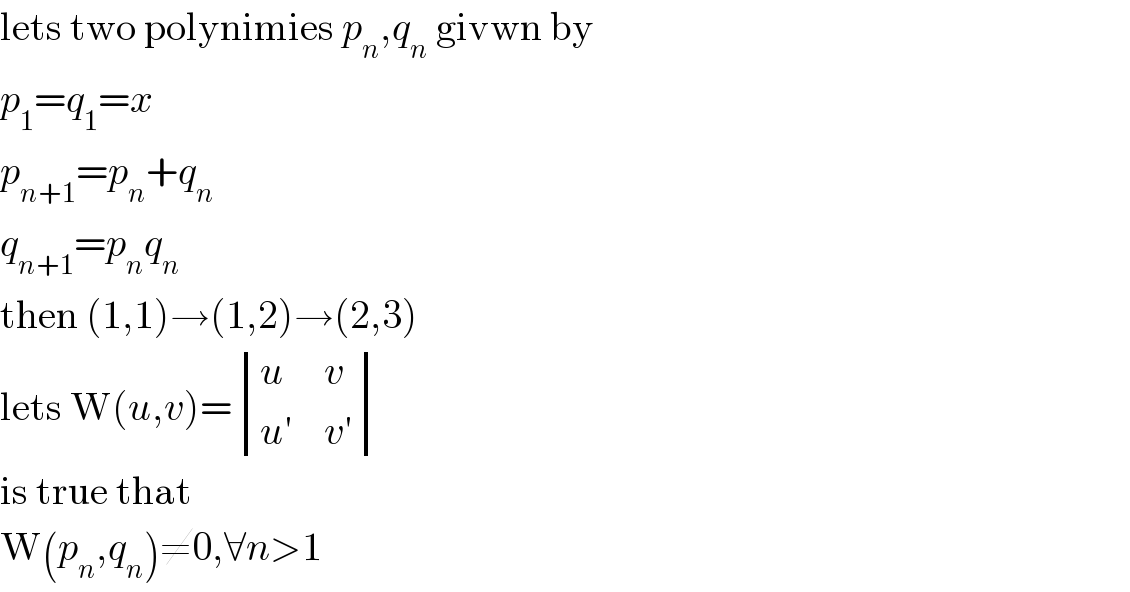
$$\mathrm{lets}\:\mathrm{two}\:\mathrm{polynimies}\:{p}_{{n}} ,{q}_{{n}} \:\mathrm{givwn}\:\mathrm{by} \\ $$ $${p}_{\mathrm{1}} ={q}_{\mathrm{1}} ={x} \\ $$ $${p}_{{n}+\mathrm{1}} ={p}_{{n}} +{q}_{{n}} \\ $$ $${q}_{{n}+\mathrm{1}} ={p}_{{n}} {q}_{{n}} \\ $$ $$\mathrm{then}\:\left(\mathrm{1},\mathrm{1}\right)\rightarrow\left(\mathrm{1},\mathrm{2}\right)\rightarrow\left(\mathrm{2},\mathrm{3}\right) \\ $$ $$\mathrm{lets}\:\mathrm{W}\left({u},{v}\right)=\begin{vmatrix}{{u}}&{{v}}\\{{u}'}&{{v}'}\end{vmatrix} \\ $$ $$\mathrm{is}\:\mathrm{true}\:\mathrm{that} \\ $$ $$\mathrm{W}\left({p}_{{n}} ,{q}_{{n}} \right)\neq\mathrm{0},\forall{n}>\mathrm{1} \\ $$
Commented byRasheed Soomro last updated on 12/Oct/15
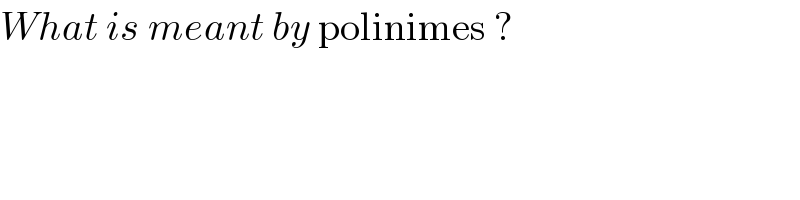
$${What}\:{is}\:{meant}\:{by}\:\mathrm{polinimes}\:? \\ $$
Commented by123456 last updated on 12/Oct/15

$$\mathrm{typo} \\ $$
Commented by112358 last updated on 17/Oct/15
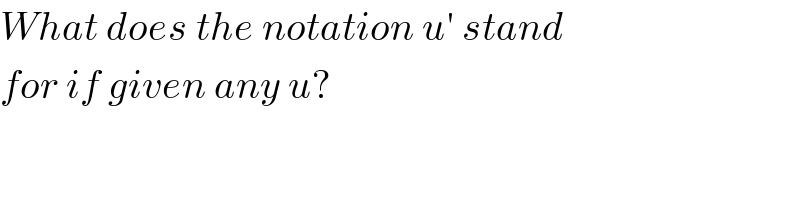
$${What}\:{does}\:{the}\:{notation}\:{u}'\:{stand} \\ $$ $${for}\:{if}\:{given}\:{any}\:{u}?\: \\ $$
Commented by123456 last updated on 17/Oct/15

$${u}'=\frac{{du}}{{dt}}={u}_{{t}} =\frac{\partial{u}}{\partial{t}} \\ $$ $$\mathrm{derivate} \\ $$
Commented by112358 last updated on 18/Oct/15
$${Thanks}\:{for}\:{explanation}. \\ $$
