
Question Number 184378 by Ml last updated on 05/Jan/23
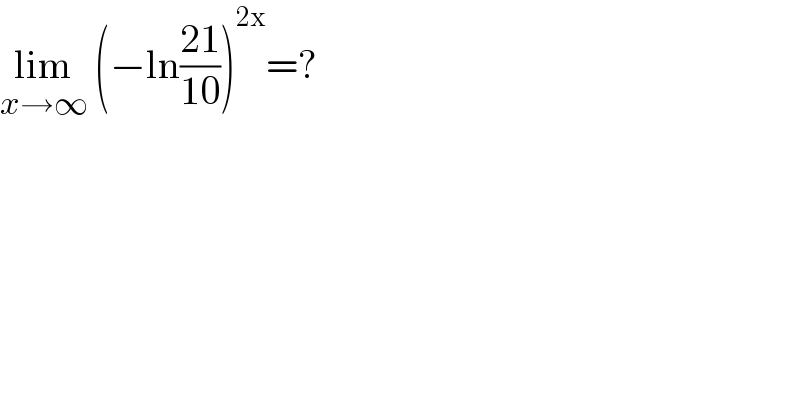
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(−\mathrm{ln}\frac{\mathrm{21}}{\mathrm{10}}\right)^{\mathrm{2x}} =? \\ $$
Answered by SEKRET last updated on 05/Jan/23

$$\mathrm{0} \\ $$$$ \\ $$
Commented by Ml last updated on 05/Jan/23

$$\mathrm{solution} \\ $$
Answered by JDamian last updated on 05/Jan/23

$$\cancel{\infty}\:{wrong} \\ $$
Commented by Ml last updated on 05/Jan/23

$$\mathrm{solution} \\ $$
Answered by Frix last updated on 06/Jan/23
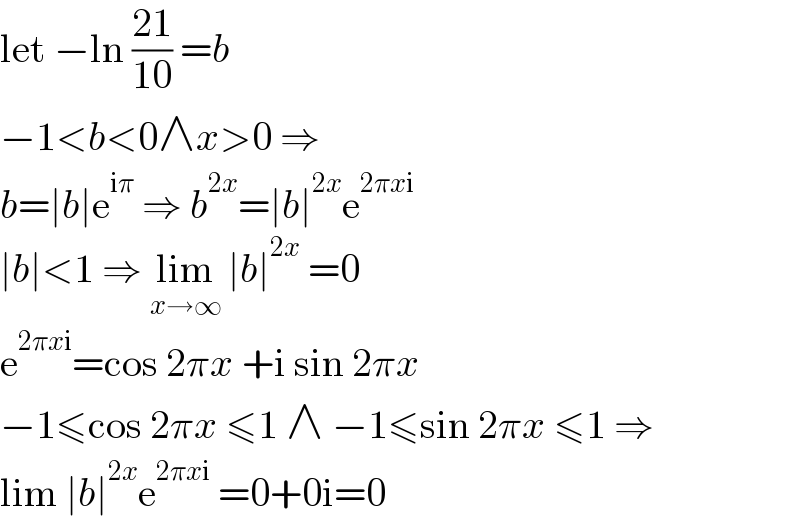
$$\mathrm{let}\:−\mathrm{ln}\:\frac{\mathrm{21}}{\mathrm{10}}\:={b} \\ $$$$−\mathrm{1}<{b}<\mathrm{0}\wedge{x}>\mathrm{0}\:\Rightarrow \\ $$$${b}=\mid{b}\mid\mathrm{e}^{\mathrm{i}\pi} \:\Rightarrow\:{b}^{\mathrm{2}{x}} =\mid{b}\mid^{\mathrm{2}{x}} \mathrm{e}^{\mathrm{2}\pi{x}\mathrm{i}} \\ $$$$\mid{b}\mid<\mathrm{1}\:\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mid{b}\mid^{\mathrm{2}{x}} \:=\mathrm{0} \\ $$$$\mathrm{e}^{\mathrm{2}\pi{x}\mathrm{i}} =\mathrm{cos}\:\mathrm{2}\pi{x}\:+\mathrm{i}\:\mathrm{sin}\:\mathrm{2}\pi{x} \\ $$$$−\mathrm{1}\leqslant\mathrm{cos}\:\mathrm{2}\pi{x}\:\leqslant\mathrm{1}\:\wedge\:−\mathrm{1}\leqslant\mathrm{sin}\:\mathrm{2}\pi{x}\:\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}\:\mid{b}\mid^{\mathrm{2}{x}} \mathrm{e}^{\mathrm{2}\pi{x}\mathrm{i}} \:=\mathrm{0}+\mathrm{0i}=\mathrm{0} \\ $$
