
Question Number 184370 by cherokeesay last updated on 05/Jan/23
Commented by cherokeesay last updated on 05/Jan/23
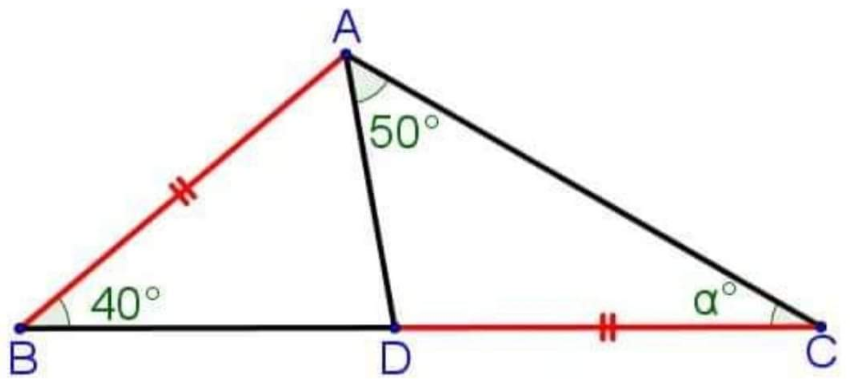
on demande la mesure de alpha :
Answered by som(math1967) last updated on 05/Jan/23
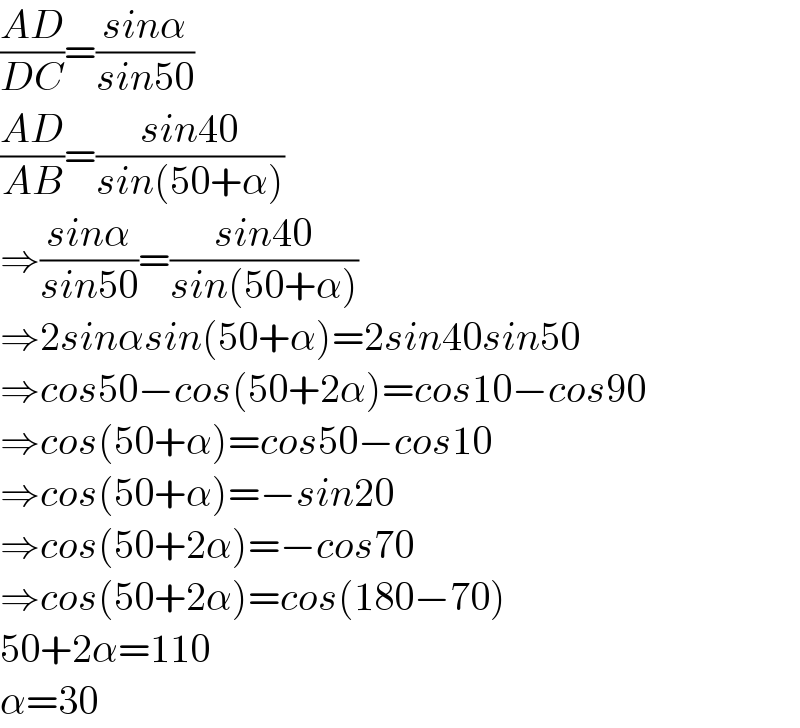
$$\frac{{AD}}{{DC}}=\frac{{sin}\alpha}{{sin}\mathrm{50}} \\ $$$$\frac{{AD}}{{AB}}=\frac{{sin}\mathrm{40}}{{sin}\left(\mathrm{50}+\alpha\right)} \\ $$$$\Rightarrow\frac{{sin}\alpha}{{sin}\mathrm{50}}=\frac{{sin}\mathrm{40}}{{sin}\left(\mathrm{50}+\alpha\right)} \\ $$$$\Rightarrow\mathrm{2}{sin}\alpha{sin}\left(\mathrm{50}+\alpha\right)=\mathrm{2}{sin}\mathrm{40}{sin}\mathrm{50} \\ $$$$\Rightarrow{cos}\mathrm{50}−{cos}\left(\mathrm{50}+\mathrm{2}\alpha\right)={cos}\mathrm{10}−{cos}\mathrm{90} \\ $$$$\Rightarrow{cos}\left(\mathrm{50}+\alpha\right)={cos}\mathrm{50}−{cos}\mathrm{10} \\ $$$$\Rightarrow{cos}\left(\mathrm{50}+\alpha\right)=−{sin}\mathrm{20} \\ $$$$\Rightarrow{cos}\left(\mathrm{50}+\mathrm{2}\alpha\right)=−{cos}\mathrm{70} \\ $$$$\Rightarrow{cos}\left(\mathrm{50}+\mathrm{2}\alpha\right)={cos}\left(\mathrm{180}−\mathrm{70}\right) \\ $$$$\mathrm{50}+\mathrm{2}\alpha=\mathrm{110} \\ $$$$\alpha=\mathrm{30} \\ $$
Commented by cherokeesay last updated on 05/Jan/23

$${thank}\:{you}\:{sir}\:! \\ $$
