
Question Number 184356 by yaslm last updated on 05/Jan/23
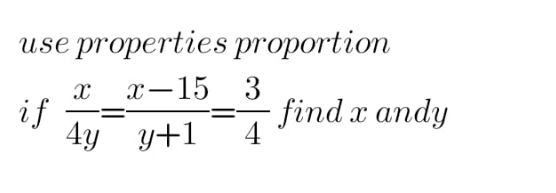
Answered by greougoury555 last updated on 05/Jan/23
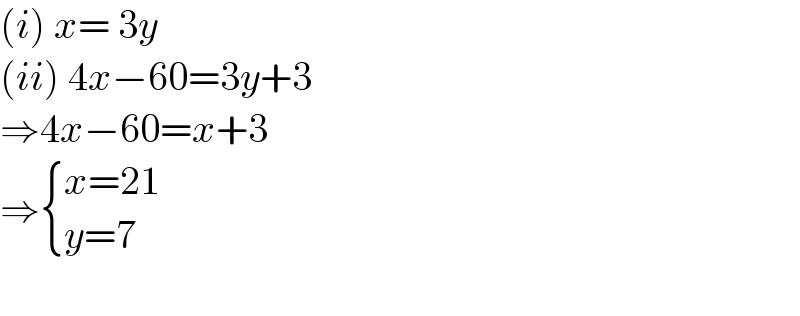
$$\left({i}\right)\:{x}=\:\mathrm{3}{y} \\ $$$$\left({ii}\right)\:\mathrm{4}{x}−\mathrm{60}=\mathrm{3}{y}+\mathrm{3} \\ $$$$\Rightarrow\mathrm{4}{x}−\mathrm{60}={x}+\mathrm{3} \\ $$$$\Rightarrow\begin{cases}{{x}=\mathrm{21}}\\{{y}=\mathrm{7}}\end{cases} \\ $$$$ \\ $$
Answered by mr W last updated on 05/Jan/23
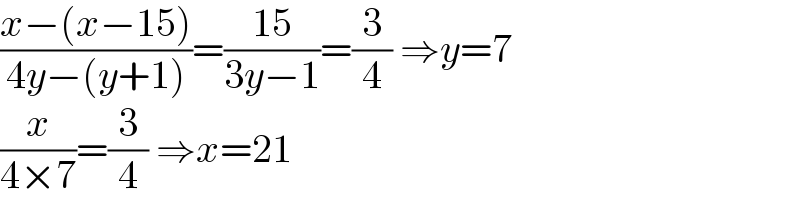
$$\frac{{x}−\left({x}−\mathrm{15}\right)}{\mathrm{4}{y}−\left({y}+\mathrm{1}\right)}=\frac{\mathrm{15}}{\mathrm{3}{y}−\mathrm{1}}=\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow{y}=\mathrm{7} \\ $$$$\frac{{x}}{\mathrm{4}×\mathrm{7}}=\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow{x}=\mathrm{21} \\ $$
