
Question Number 184351 by mr W last updated on 05/Jan/23
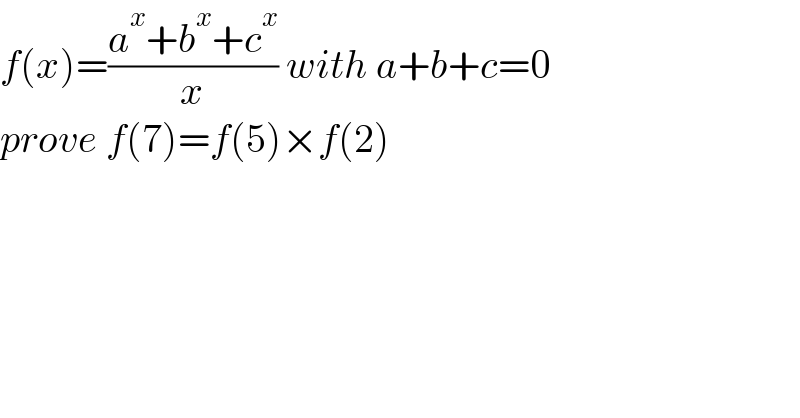
$${f}\left({x}\right)=\frac{{a}^{{x}} +{b}^{{x}} +{c}^{{x}} }{{x}}\:{with}\:{a}+{b}+{c}=\mathrm{0} \\ $$$${prove}\:{f}\left(\mathrm{7}\right)={f}\left(\mathrm{5}\right)×{f}\left(\mathrm{2}\right) \\ $$
Answered by greougoury555 last updated on 05/Jan/23

$$\:{f}\left({x}\right)=\frac{{a}^{{x}} +{b}^{{x}} +\left(−{a}−{b}\right)^{{x}} }{{x}} \\ $$$$\:\begin{cases}{{f}\left(\mathrm{7}\right)=\frac{{a}^{\mathrm{7}} +{b}^{\mathrm{7}} −\left({a}+{b}\right)^{\mathrm{7}} }{\mathrm{7}}}\\{{f}\left(\mathrm{5}\right)=\frac{{a}^{\mathrm{5}} +{b}^{\mathrm{5}} −\left({a}+{b}\right)^{\mathrm{5}} }{\mathrm{5}}}\\{{f}\left(\mathrm{2}\right)=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}}}\end{cases} \\ $$$$\:{f}\left(\mathrm{2}\right)=\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right)}{\mathrm{2}}\:=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab} \\ $$$$\:{f}\left(\mathrm{5}\right)=\frac{−\left(\mathrm{5}{a}^{\mathrm{4}} {b}+\mathrm{10}{a}^{\mathrm{3}} {b}^{\mathrm{2}} +\mathrm{10}{a}^{\mathrm{2}} {b}^{\mathrm{3}} +\mathrm{5}{ab}^{\mathrm{4}} \right)}{\mathrm{5}} \\ $$$$\:{f}\left(\mathrm{5}\right)=−{ab}\left({a}^{\mathrm{3}} +\mathrm{2}{a}^{\mathrm{2}} {b}+\mathrm{2}{ab}^{\mathrm{2}} +{b}^{\mathrm{3}} \right) \\ $$$$\:{f}\left(\mathrm{7}\right)=\frac{−\left(\mathrm{7}{a}^{\mathrm{6}} {b}+\mathrm{21}{a}^{\mathrm{5}} {b}^{\mathrm{2}} +\mathrm{35}{a}^{\mathrm{4}} {b}^{\mathrm{3}} +\mathrm{35}{a}^{\mathrm{3}} {b}^{\mathrm{4}} +\mathrm{21}{a}^{\mathrm{2}} {b}^{\mathrm{5}} +\mathrm{7}{ab}^{\mathrm{6}} \right)}{\mathrm{7}} \\ $$$$\:{f}\left(\mathrm{7}\right)=−{ab}\left({a}^{\mathrm{5}} +\mathrm{3}{a}^{\mathrm{4}} {b}+\mathrm{5}{a}^{\mathrm{3}} {b}^{\mathrm{2}} +\mathrm{5}{a}^{\mathrm{2}} {b}^{\mathrm{3}} +\mathrm{3}{ab}^{\mathrm{4}} +{b}^{\mathrm{5}} \right) \\ $$
Commented by mr W last updated on 06/Jan/23
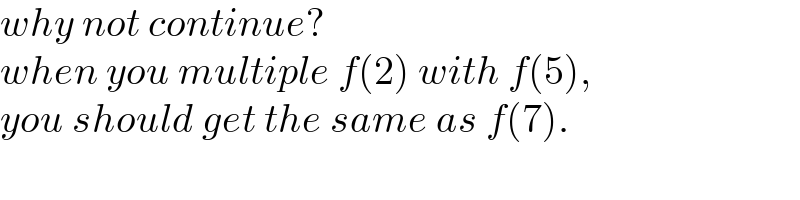
$${why}\:{not}\:{continue}? \\ $$$${when}\:{you}\:{multiple}\:{f}\left(\mathrm{2}\right)\:{with}\:{f}\left(\mathrm{5}\right), \\ $$$${you}\:{should}\:{get}\:{the}\:{same}\:{as}\:{f}\left(\mathrm{7}\right). \\ $$
Answered by Rasheed.Sindhi last updated on 05/Jan/23

$${f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{2}\right)=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left({a}+{b}+{c}\right)^{\mathrm{2}} −\mathrm{2}\left({ab}+{bc}+{ca}\right)}{\mathrm{2}} \\ $$$${f}\left(\mathrm{2}\right)=−{ab}−{bc}−{ca} \\ $$$${f}\left(\mathrm{3}\right)=\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${f}\left(\mathrm{3}\right)−{abc}=\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }{\mathrm{3}}−{abc} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:=\frac{\left({a}+{b}+{c}\right)\left(...\right)}{\mathrm{3}}=\mathrm{0} \\ $$$${f}\left(\mathrm{3}\right)={abc} \\ $$$${Consider}\:{a}\:{polynomial}\:{equation} \\ $$$${with}\:{three}\:{roots}:\:{a},{b},{c} \\ $$$${x}^{\mathrm{3}} −\left({a}+{b}+{c}\right){x}^{\mathrm{2}} +\left({ab}+{bc}+{ca}\right){x}−{abc}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\left(−{ab}−{bc}−{ca}\right){x}−{abc}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −{xf}\left(\mathrm{2}\right)−{f}\left(\mathrm{3}\right)=\mathrm{0} \\ $$$$.... \\ $$
Answered by Rasheed.Sindhi last updated on 06/Jan/23
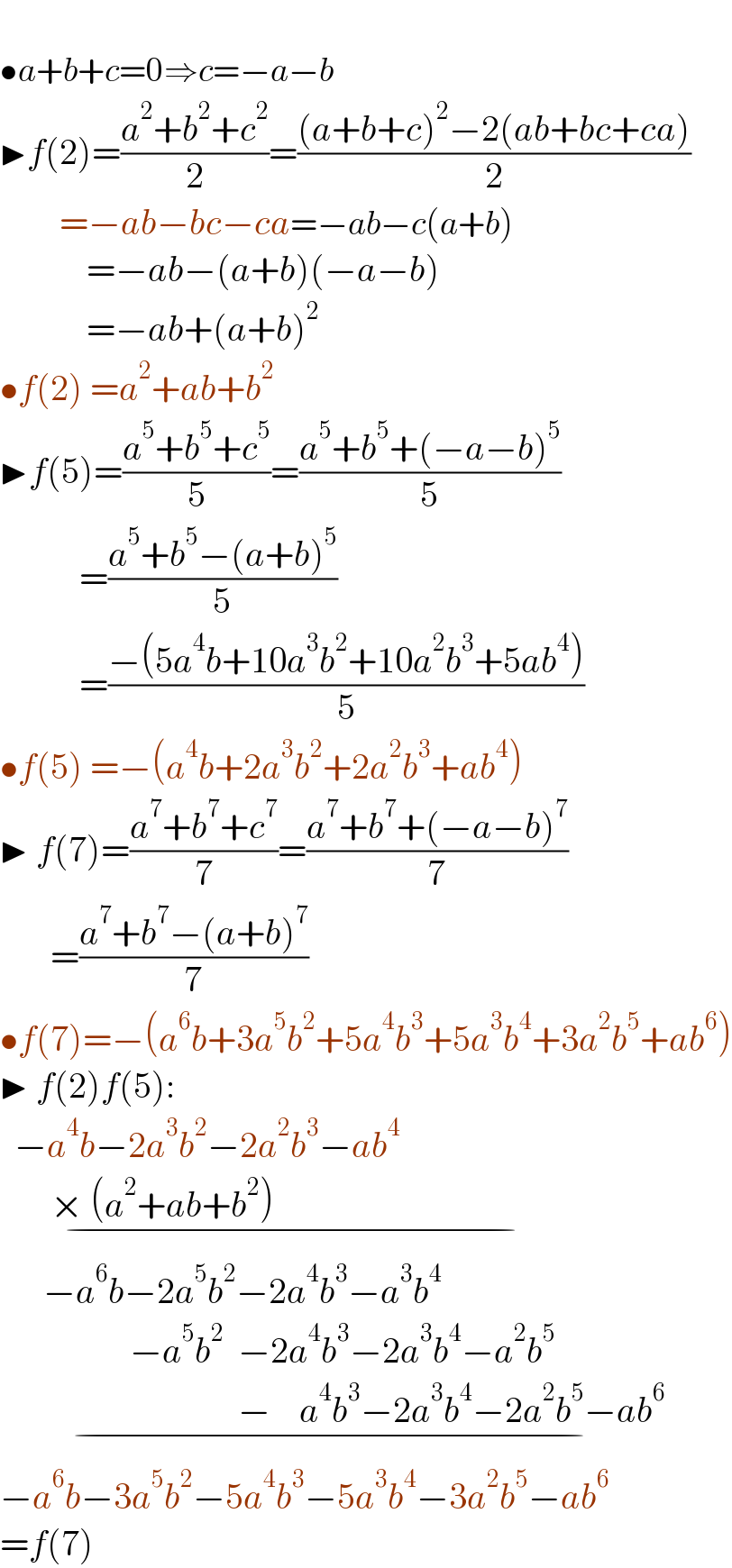
$$ \\ $$$$\bullet{a}+{b}+{c}=\mathrm{0}\Rightarrow{c}=−{a}−{b} \\ $$$$\blacktriangleright{f}\left(\mathrm{2}\right)=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left({a}+{b}+{c}\right)^{\mathrm{2}} −\mathrm{2}\left({ab}+{bc}+{ca}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−{ab}−{bc}−{ca}=−{ab}−{c}\left({a}+{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−{ab}−\left({a}+{b}\right)\left(−{a}−{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−{ab}+\left({a}+{b}\right)^{\mathrm{2}} \\ $$$$\bullet{f}\left(\mathrm{2}\right)\:={a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \\ $$$$\blacktriangleright{f}\left(\mathrm{5}\right)=\frac{{a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} }{\mathrm{5}}=\frac{{a}^{\mathrm{5}} +{b}^{\mathrm{5}} +\left(−{a}−{b}\right)^{\mathrm{5}} }{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{{a}^{\mathrm{5}} +{b}^{\mathrm{5}} −\left({a}+{b}\right)^{\mathrm{5}} }{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{−\left(\mathrm{5}{a}^{\mathrm{4}} {b}+\mathrm{10}{a}^{\mathrm{3}} {b}^{\mathrm{2}} +\mathrm{10}{a}^{\mathrm{2}} {b}^{\mathrm{3}} +\mathrm{5}{ab}^{\mathrm{4}} \right)}{\mathrm{5}} \\ $$$$\bullet{f}\left(\mathrm{5}\right)\:=−\left({a}^{\mathrm{4}} {b}+\mathrm{2}{a}^{\mathrm{3}} {b}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{3}} +{ab}^{\mathrm{4}} \right) \\ $$$$\blacktriangleright\:{f}\left(\mathrm{7}\right)=\frac{{a}^{\mathrm{7}} +{b}^{\mathrm{7}} +{c}^{\mathrm{7}} }{\mathrm{7}}=\frac{{a}^{\mathrm{7}} +{b}^{\mathrm{7}} +\left(−{a}−{b}\right)^{\mathrm{7}} }{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:=\frac{{a}^{\mathrm{7}} +{b}^{\mathrm{7}} −\left({a}+{b}\right)^{\mathrm{7}} }{\mathrm{7}} \\ $$$$\bullet{f}\left(\mathrm{7}\right)=−\left({a}^{\mathrm{6}} {b}+\mathrm{3}{a}^{\mathrm{5}} {b}^{\mathrm{2}} +\mathrm{5}{a}^{\mathrm{4}} {b}^{\mathrm{3}} +\mathrm{5}{a}^{\mathrm{3}} {b}^{\mathrm{4}} +\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{5}} +{ab}^{\mathrm{6}} \right) \\ $$$$\blacktriangleright\:{f}\left(\mathrm{2}\right){f}\left(\mathrm{5}\right): \\ $$$$\:\:−{a}^{\mathrm{4}} {b}−\mathrm{2}{a}^{\mathrm{3}} {b}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{3}} −{ab}^{\mathrm{4}} \:\:\: \\ $$$$\underset{−} {\:\:\:\:\:\:\:×\:\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} \\ $$$$\:\:\:\:\:\:−{a}^{\mathrm{6}} {b}−\mathrm{2}{a}^{\mathrm{5}} {b}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{4}} {b}^{\mathrm{3}} −{a}^{\mathrm{3}} {b}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{a}^{\mathrm{5}} {b}^{\mathrm{2}} \:\:−\mathrm{2}{a}^{\mathrm{4}} {b}^{\mathrm{3}} −\mathrm{2}{a}^{\mathrm{3}} {b}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{5}} \\ $$$$\underset{−} {\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:{a}^{\mathrm{4}} {b}^{\mathrm{3}} −\mathrm{2}{a}^{\mathrm{3}} {b}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{5}} −{ab}^{\mathrm{6}} \:\:\:} \\ $$$$−{a}^{\mathrm{6}} {b}−\mathrm{3}{a}^{\mathrm{5}} {b}^{\mathrm{2}} −\mathrm{5}{a}^{\mathrm{4}} {b}^{\mathrm{3}} −\mathrm{5}{a}^{\mathrm{3}} {b}^{\mathrm{4}} −\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{5}} −{ab}^{\mathrm{6}} \\ $$$$={f}\left(\mathrm{7}\right) \\ $$
Commented by mr W last updated on 06/Jan/23

$${fine}! \\ $$$${thanks}\:{for}\:{the}\:{interest}\:{sir}! \\ $$
Answered by mr W last updated on 06/Jan/23
![Method I (a+b+c)^2 =a^2 +b^2 +c^2 +2(ab+bc+ca)=0 ⇒a^2 +b^2 +c^2 =−2(ab+bc+ca) ⇒f(2)=((a^2 +b^2 +c^2 )/2)=−(ab+bc+ca) (a+b+c)^3 =a^3 +b^3 +c^2 +3(a+b+c)(ab+bc+ca)−3abc=0 ⇒a^3 +b^3 +c^3 =3abc ⇒f(3)=((a^3 +b^3 +c^3 )/3)=abc (a^2 +b^2 +c^2 )(a^3 +b^3 +c^2 )=−6(ab+bc+ca)abc a^5 +b^5 +c^5 +(a^2 b^2 +b^2 c^2 +c^2 a^2 )(a+b+c)−abc(ab+bc+ca)=−6(ab+bc+ca)abc ⇒a^5 +b^5 +c^5 =−5(ab+bc+ca)abc ⇒f(5)=((a^5 +b^5 +c^5 )/5)=−(ab+bc+ca)abc (a^2 +b^2 +c^2 )(a^5 +b^5 +c^5 )=10(ab+bc+ca)^2 abc a^7 +b^7 +c^7 +(a^2 b^2 +b^2 c^2 +c^2 a^2 )(a^3 +b^3 +c^3 )−a^2 b^2 c^2 (a+b+c)=10(ab+bc+ca)^2 abc a^7 +b^7 +c^7 +3abc(a^2 b^2 +b^2 c^2 +c^2 a^2 )=10(ab+bc+ca)^2 abc a^7 +b^7 +c^7 +3abc[(ab+bc+ca)^2 −2abc(a+b+c)]=10(ab+bc+ca)^2 abc a^7 +b^7 +c^7 +3abc(ab+bc+ca)^2 =10(ab+bc+ca)^2 abc ⇒a^7 +b^7 +c^7 =7(ab+bc+ca)^2 abc ⇒f(7)=((a^7 +b^7 +c^7 )/7)=(ab+bc+ca)^2 abc f(2)×f(5)=(ab+bc+ca)^2 abc=f(7) ✓](Q184422.png)
$$\boldsymbol{{Method}}\:\boldsymbol{{I}} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right)=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =−\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\Rightarrow{f}\left(\mathrm{2}\right)=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}}=−\left({ab}+{bc}+{ca}\right) \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{2}} +\mathrm{3}\left({a}+{b}+{c}\right)\left({ab}+{bc}+{ca}\right)−\mathrm{3}{abc}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{3}{abc} \\ $$$$\Rightarrow{f}\left(\mathrm{3}\right)=\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }{\mathrm{3}}={abc} \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{2}} \right)=−\mathrm{6}\left({ab}+{bc}+{ca}\right){abc} \\ $$$${a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} +\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)\left({a}+{b}+{c}\right)−{abc}\left({ab}+{bc}+{ca}\right)=−\mathrm{6}\left({ab}+{bc}+{ca}\right){abc} \\ $$$$\Rightarrow{a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} =−\mathrm{5}\left({ab}+{bc}+{ca}\right){abc} \\ $$$$\Rightarrow{f}\left(\mathrm{5}\right)=\frac{{a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} }{\mathrm{5}}=−\left({ab}+{bc}+{ca}\right){abc} \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} \right)=\mathrm{10}\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} {abc} \\ $$$${a}^{\mathrm{7}} +{b}^{\mathrm{7}} +{c}^{\mathrm{7}} +\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \right)−{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \left({a}+{b}+{c}\right)=\mathrm{10}\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} {abc} \\ $$$${a}^{\mathrm{7}} +{b}^{\mathrm{7}} +{c}^{\mathrm{7}} +\mathrm{3}{abc}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)=\mathrm{10}\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} {abc} \\ $$$${a}^{\mathrm{7}} +{b}^{\mathrm{7}} +{c}^{\mathrm{7}} +\mathrm{3}{abc}\left[\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} −\mathrm{2}{abc}\left({a}+{b}+{c}\right)\right]=\mathrm{10}\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} {abc} \\ $$$${a}^{\mathrm{7}} +{b}^{\mathrm{7}} +{c}^{\mathrm{7}} +\mathrm{3}{abc}\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} =\mathrm{10}\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} {abc} \\ $$$$\Rightarrow{a}^{\mathrm{7}} +{b}^{\mathrm{7}} +{c}^{\mathrm{7}} =\mathrm{7}\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} {abc} \\ $$$$\Rightarrow{f}\left(\mathrm{7}\right)=\frac{{a}^{\mathrm{7}} +{b}^{\mathrm{7}} +{c}^{\mathrm{7}} }{\mathrm{7}}=\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} {abc} \\ $$$${f}\left(\mathrm{2}\right)×{f}\left(\mathrm{5}\right)=\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} {abc}={f}\left(\mathrm{7}\right)\:\checkmark \\ $$
Commented by mr W last updated on 06/Jan/23
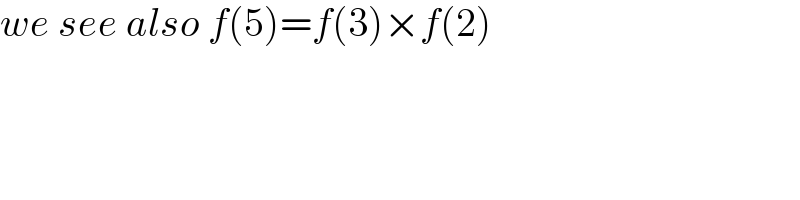
$${we}\:{see}\:{also}\:{f}\left(\mathrm{5}\right)={f}\left(\mathrm{3}\right)×{f}\left(\mathrm{2}\right) \\ $$
Answered by mr W last updated on 06/Jan/23
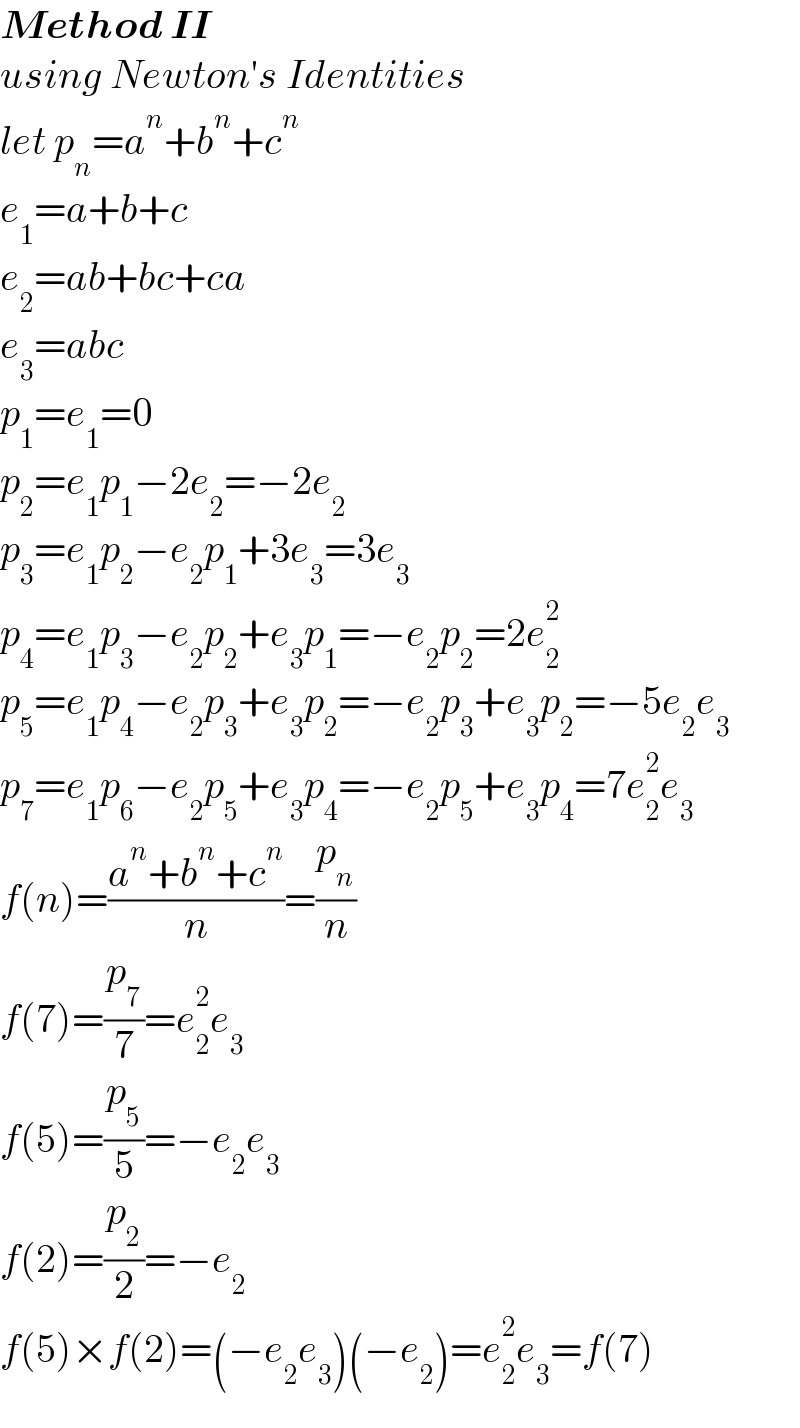
$$\boldsymbol{{Method}}\:\boldsymbol{{II}} \\ $$$${using}\:{Newton}'{s}\:{Identities} \\ $$$${let}\:{p}_{{n}} ={a}^{{n}} +{b}^{{n}} +{c}^{{n}} \\ $$$${e}_{\mathrm{1}} ={a}+{b}+{c} \\ $$$${e}_{\mathrm{2}} ={ab}+{bc}+{ca} \\ $$$${e}_{\mathrm{3}} ={abc} \\ $$$${p}_{\mathrm{1}} ={e}_{\mathrm{1}} =\mathrm{0} \\ $$$${p}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} =−\mathrm{2}{e}_{\mathrm{2}} \\ $$$${p}_{\mathrm{3}} ={e}_{\mathrm{1}} {p}_{\mathrm{2}} −{e}_{\mathrm{2}} {p}_{\mathrm{1}} +\mathrm{3}{e}_{\mathrm{3}} =\mathrm{3}{e}_{\mathrm{3}} \\ $$$${p}_{\mathrm{4}} ={e}_{\mathrm{1}} {p}_{\mathrm{3}} −{e}_{\mathrm{2}} {p}_{\mathrm{2}} +{e}_{\mathrm{3}} {p}_{\mathrm{1}} =−{e}_{\mathrm{2}} {p}_{\mathrm{2}} =\mathrm{2}{e}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${p}_{\mathrm{5}} ={e}_{\mathrm{1}} {p}_{\mathrm{4}} −{e}_{\mathrm{2}} {p}_{\mathrm{3}} +{e}_{\mathrm{3}} {p}_{\mathrm{2}} =−{e}_{\mathrm{2}} {p}_{\mathrm{3}} +{e}_{\mathrm{3}} {p}_{\mathrm{2}} =−\mathrm{5}{e}_{\mathrm{2}} {e}_{\mathrm{3}} \\ $$$${p}_{\mathrm{7}} ={e}_{\mathrm{1}} {p}_{\mathrm{6}} −{e}_{\mathrm{2}} {p}_{\mathrm{5}} +{e}_{\mathrm{3}} {p}_{\mathrm{4}} =−{e}_{\mathrm{2}} {p}_{\mathrm{5}} +{e}_{\mathrm{3}} {p}_{\mathrm{4}} =\mathrm{7}{e}_{\mathrm{2}} ^{\mathrm{2}} {e}_{\mathrm{3}} \\ $$$${f}\left({n}\right)=\frac{{a}^{{n}} +{b}^{{n}} +{c}^{{n}} }{{n}}=\frac{{p}_{{n}} }{{n}} \\ $$$${f}\left(\mathrm{7}\right)=\frac{{p}_{\mathrm{7}} }{\mathrm{7}}={e}_{\mathrm{2}} ^{\mathrm{2}} {e}_{\mathrm{3}} \\ $$$${f}\left(\mathrm{5}\right)=\frac{{p}_{\mathrm{5}} }{\mathrm{5}}=−{e}_{\mathrm{2}} {e}_{\mathrm{3}} \\ $$$${f}\left(\mathrm{2}\right)=\frac{{p}_{\mathrm{2}} }{\mathrm{2}}=−{e}_{\mathrm{2}} \\ $$$${f}\left(\mathrm{5}\right)×{f}\left(\mathrm{2}\right)=\left(−{e}_{\mathrm{2}} {e}_{\mathrm{3}} \right)\left(−{e}_{\mathrm{2}} \right)={e}_{\mathrm{2}} ^{\mathrm{2}} {e}_{\mathrm{3}} ={f}\left(\mathrm{7}\right) \\ $$
