
Question Number 184329 by greougoury555 last updated on 05/Jan/23
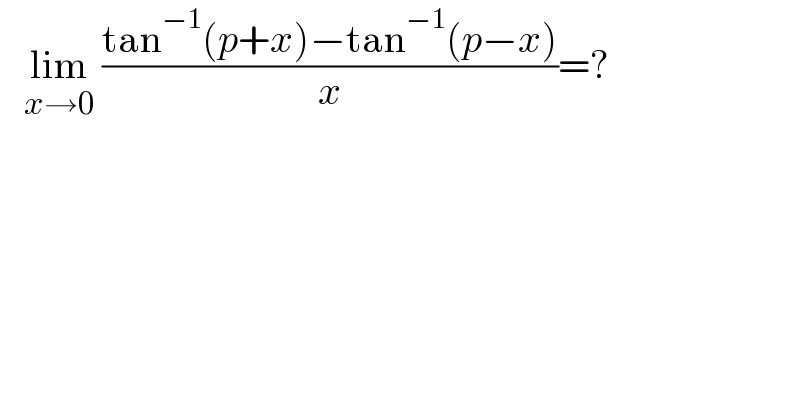
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({p}+{x}\right)−\mathrm{tan}^{−\mathrm{1}} \left({p}−{x}\right)}{{x}}=? \\ $$
Answered by SEKRET last updated on 05/Jan/23

$$\:\:\frac{\mathrm{2}}{\mathrm{1}+\boldsymbol{\mathrm{p}}^{\mathrm{2}} } \\ $$
Answered by mr W last updated on 05/Jan/23
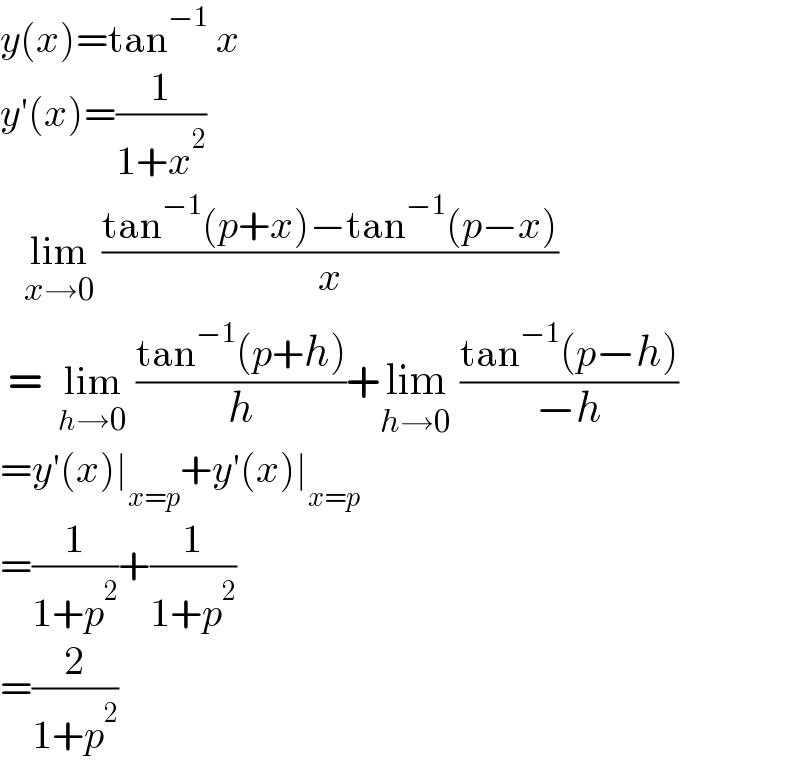
$${y}\left({x}\right)=\mathrm{tan}^{−\mathrm{1}} \:{x} \\ $$$${y}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({p}+{x}\right)−\mathrm{tan}^{−\mathrm{1}} \left({p}−{x}\right)}{{x}} \\ $$$$\:=\:\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({p}+{h}\right)}{{h}}+\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({p}−{h}\right)}{−{h}} \\ $$$$={y}'\left({x}\right)\mid_{{x}={p}} +{y}'\left({x}\right)\mid_{{x}={p}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}+{p}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}+{p}^{\mathrm{2}} } \\ $$
Answered by cortano1 last updated on 05/Jan/23

$$\:{Find}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({p}+{x}\right)−\mathrm{tan}^{−\mathrm{1}} \left({p}−{x}\right)}{{x}} \\ $$$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({p}+{x}\right)−\mathrm{tan}^{−\mathrm{1}} {p}}{{x}}\:+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}^{−\mathrm{1}} {p}−\mathrm{tan}^{−\mathrm{1}} \left({p}−{x}\right)}{{x}} \\ $$$${L}_{\mathrm{1}} =\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({p}+{x}\right)−\mathrm{tan}^{−\mathrm{1}} {p}}{{x}} \\ $$$${L}_{\mathrm{1}} =\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{{x}\left\{\mathrm{1}+{p}\left({p}+{x}\right)\right\}}\:=\:\frac{\mathrm{1}}{{p}^{\mathrm{2}} +\mathrm{1}} \\ $$$${L}_{\mathrm{2}} =\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}^{−\mathrm{1}} {p}−\mathrm{tan}^{−\mathrm{1}} \left({p}−{x}\right)}{{x}} \\ $$$${L}_{\mathrm{2}} =\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{{x}\left\{\mathrm{1}+{p}\left({p}−{x}\right)\right\}}\:=\:\frac{\mathrm{1}}{{p}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\therefore\:{L}={L}_{\mathrm{1}} +{L}_{\mathrm{2}} =\:\frac{\mathrm{2}}{{p}^{\mathrm{2}} +\mathrm{1}}\: \\ $$
