
Question Number 184302 by cortano1 last updated on 05/Jan/23
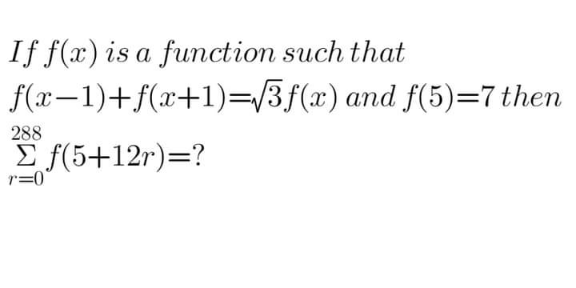
Answered by mr W last updated on 05/Jan/23

$${say}\:{f}\left({x}\right)={Ap}^{{x}} \\ $$$${Ap}^{{x}−\mathrm{1}} +{Ap}^{{x}+\mathrm{1}} =\sqrt{\mathrm{3}}{Ap}^{{x}} \\ $$$$\mathrm{1}+{p}^{\mathrm{2}} =\sqrt{\mathrm{3}}{p} \\ $$$${p}^{\mathrm{2}} −\sqrt{\mathrm{3}}{p}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{p}=\frac{\sqrt{\mathrm{3}}\pm{i}}{\mathrm{2}}={e}^{\pm\frac{\pi{i}}{\mathrm{6}}} \\ $$$$\Rightarrow{f}\left({x}\right)={Ae}^{\frac{\pi{xi}}{\mathrm{6}}} +{Be}^{−\frac{\pi{xi}}{\mathrm{6}}} \\ $$$${f}\left(\mathrm{5}+\mathrm{12}{r}\right)={Ae}^{\frac{\pi\left(\mathrm{5}+\mathrm{12}{r}\right){i}}{\mathrm{6}}} +{Be}^{−\frac{\pi\left(\mathrm{5}+\mathrm{12}{r}\right){i}}{\mathrm{6}}} \\ $$$${f}\left(\mathrm{5}+\mathrm{12}{r}\right)={Ae}^{\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+\mathrm{2}{r}\pi\right){i}} +{Be}^{−\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+\mathrm{2}{r}\pi\right){i}} \\ $$$${f}\left(\mathrm{5}+\mathrm{12}{r}\right)={Ae}^{\left(\frac{\mathrm{5}\pi}{\mathrm{6}}\right){i}} +{Be}^{−\left(\frac{\mathrm{5}\pi}{\mathrm{6}}\right){i}} ={f}\left(\mathrm{5}\right)=\mathrm{7} \\ $$$$\underset{{r}=\mathrm{0}} {\overset{\mathrm{288}} {\sum}}{f}\left(\mathrm{5}+\mathrm{12}{r}\right)=\underset{{r}=\mathrm{0}} {\overset{\mathrm{288}} {\sum}}\mathrm{7}=\mathrm{289}×\mathrm{7}=\mathrm{2023} \\ $$
Commented by cortano1 last updated on 05/Jan/23

$${nice}\:{solution} \\ $$
