
Question Number 184270 by mathlove last updated on 04/Jan/23

$$\sqrt[{\mathrm{6}}]{−\mathrm{64}}\centerdot\sqrt[{\mathrm{7}}]{−\mathrm{128}}=? \\ $$
Answered by HeferH last updated on 04/Jan/23
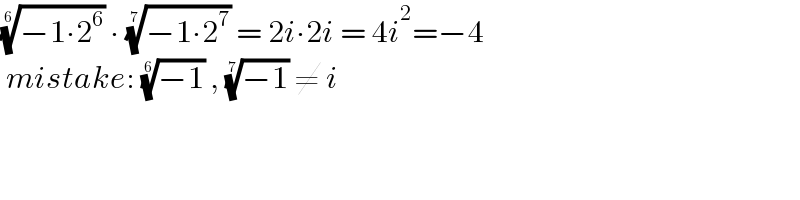
$$\sqrt[{\mathrm{6}}]{−\mathrm{1}\centerdot\mathrm{2}^{\mathrm{6}} }\:\centerdot\:\sqrt[{\mathrm{7}}]{−\mathrm{1}\centerdot\mathrm{2}^{\mathrm{7}} }\:=\:\mathrm{2}{i}\centerdot\mathrm{2}{i}\:=\:\mathrm{4}{i}^{\mathrm{2}} =−\mathrm{4} \\ $$$$\:{mistake}:\:\sqrt[{\mathrm{6}}]{−\mathrm{1}}\:,\:\sqrt[{\mathrm{7}}]{−\mathrm{1}}\:\neq\:{i} \\ $$
Commented by TheSupreme last updated on 04/Jan/23
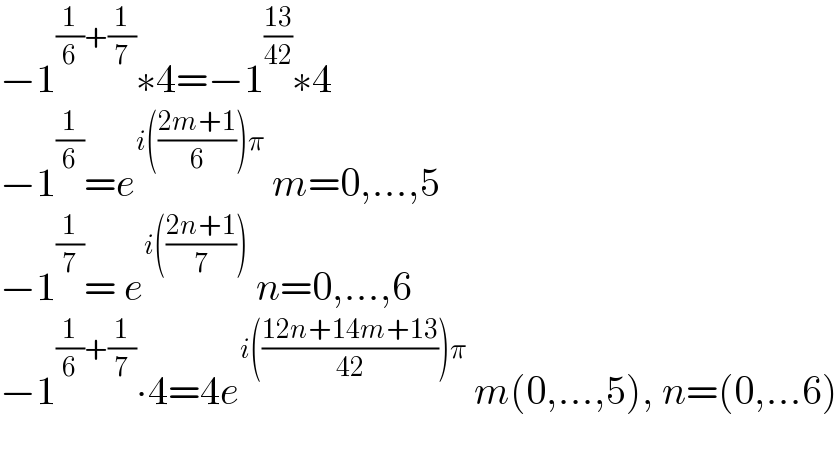
$$−\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{7}}} \ast\mathrm{4}=−\mathrm{1}^{\frac{\mathrm{13}}{\mathrm{42}}} \ast\mathrm{4} \\ $$$$−\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{6}}} ={e}^{{i}\left(\frac{\mathrm{2}{m}+\mathrm{1}}{\mathrm{6}}\right)\pi} \:{m}=\mathrm{0},...,\mathrm{5} \\ $$$$−\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{7}}} =\:{e}^{{i}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{7}}\right)} \:{n}=\mathrm{0},...,\mathrm{6} \\ $$$$−\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{7}}} \centerdot\mathrm{4}=\mathrm{4}{e}^{{i}\left(\frac{\mathrm{12}{n}+\mathrm{14}{m}+\mathrm{13}}{\mathrm{42}}\right)\pi} \:{m}\left(\mathrm{0},...,\mathrm{5}\right),\:{n}=\left(\mathrm{0},...\mathrm{6}\right) \\ $$$$ \\ $$
Commented by Frix last updated on 04/Jan/23
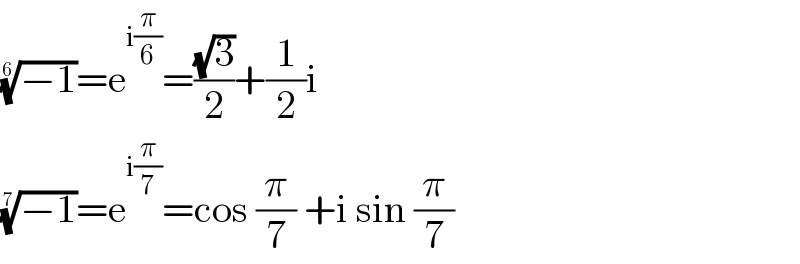
$$\sqrt[{\mathrm{6}}]{−\mathrm{1}}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{6}}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i} \\ $$$$\sqrt[{\mathrm{7}}]{−\mathrm{1}}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{7}}} =\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\:+\mathrm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{7}} \\ $$
Answered by Frix last updated on 04/Jan/23
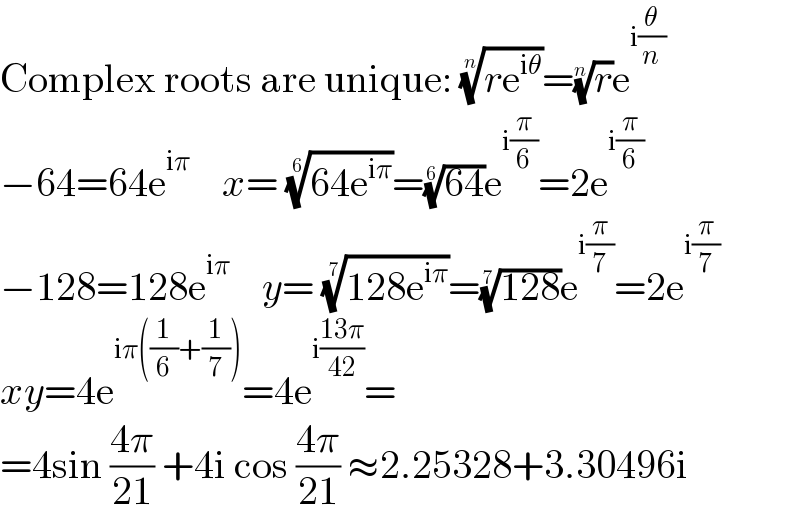
$$\mathrm{Complex}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{unique}:\:\sqrt[{{n}}]{{r}\mathrm{e}^{\mathrm{i}\theta} }=\sqrt[{{n}}]{{r}}\mathrm{e}^{\mathrm{i}\frac{\theta}{{n}}} \\ $$$$−\mathrm{64}=\mathrm{64e}^{\mathrm{i}\pi} \:\:\:\:{x}=\:\sqrt[{\mathrm{6}}]{\mathrm{64e}^{\mathrm{i}\pi} }=\sqrt[{\mathrm{6}}]{\mathrm{64}}\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{6}}} =\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{6}}} \\ $$$$−\mathrm{128}=\mathrm{128e}^{\mathrm{i}\pi} \:\:\:\:{y}=\:\sqrt[{\mathrm{7}}]{\mathrm{128e}^{\mathrm{i}\pi} }=\sqrt[{\mathrm{7}}]{\mathrm{128}}\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{7}}} =\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{7}}} \\ $$$${xy}=\mathrm{4e}^{\mathrm{i}\pi\left(\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{7}}\right)} =\mathrm{4e}^{\mathrm{i}\frac{\mathrm{13}\pi}{\mathrm{42}}} = \\ $$$$=\mathrm{4sin}\:\frac{\mathrm{4}\pi}{\mathrm{21}}\:+\mathrm{4i}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{21}}\:\approx\mathrm{2}.\mathrm{25328}+\mathrm{3}.\mathrm{30496i} \\ $$
Commented by TheSupreme last updated on 05/Jan/23
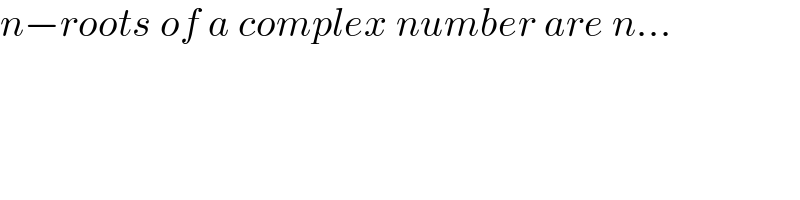
$${n}−{roots}\:{of}\:{a}\:{complex}\:{number}\:{are}\:{n}... \\ $$
Commented by Frix last updated on 05/Jan/23

$$\mathrm{No}.\:\mathrm{This}\:\mathrm{problem}\:\mathrm{had}\:\mathrm{been}\:\mathrm{explained}\:\mathrm{by} \\ $$$$\mathrm{Sir}\:\mathrm{MJS}\:\mathrm{before}. \\ $$$$\mid{z}\mid\geqslant\mathrm{0}\vee{z}\in\mathbb{C} \\ $$$$\mid{a}+{b}\mathrm{i}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\geqslant\mathrm{0} \\ $$$$\mathrm{Or}\:\mathrm{what}\:\mathrm{have}\:\mathrm{you}\:\mathrm{learned}? \\ $$$$\mathrm{A}\:\mathrm{simple}\:\mathrm{root}\:\mathrm{is}\:\mathrm{not}\:\mathrm{an}\:\mathrm{equation}.\:\mathrm{An}\:\mathrm{equation} \\ $$$$\mathrm{might}\:\mathrm{have}\:\mathrm{several}\:\mathrm{roots}\:\mathrm{but}\:\mathrm{each}\:\mathrm{root} \\ $$$$\mathrm{has}\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{value}. \\ $$$$\sqrt{\mathrm{4}}=\mathrm{2}\:\left(\mathrm{unique}\right)\:\mathrm{but}\:{x}^{\mathrm{2}} =\mathrm{4}\:\Rightarrow\:{x}=\pm\sqrt{\mathrm{4}} \\ $$$$\mathrm{The}\:\pm\:\mathrm{comes}\:\mathrm{from}\:\mathrm{the}\:\mathrm{law}\:\mathrm{of}\:\mathrm{transforming} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{not}\:\mathrm{from}``\mathrm{within}''\:\mathrm{the}\:\mathrm{root}. \\ $$$$\mathrm{Try}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{and}\:\mathrm{test}\:\mathrm{the}\:\mathrm{solution}: \\ $$$$\sqrt{{x}}=−\mathrm{2} \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{were}\:\mathrm{right}\:\mathrm{we}\:\mathrm{could}\:\mathrm{solve}\:\mathrm{this}: \\ $$$$\sqrt{{x}−\mathrm{6}}−\sqrt{{x}}=\mathrm{6} \\ $$$${x}=\frac{\mathrm{49}}{\mathrm{4}} \\ $$$$\mathrm{proof}: \\ $$$$\sqrt{\frac{\mathrm{49}}{\mathrm{4}}−\mathrm{6}}−\sqrt{\frac{\mathrm{49}}{\mathrm{4}}}=\sqrt{\frac{\mathrm{25}}{\mathrm{4}}}−\sqrt{\frac{\mathrm{49}}{\mathrm{4}}}=\pm\frac{\mathrm{5}}{\mathrm{2}}\mp\frac{\mathrm{7}}{\mathrm{2}}= \\ $$$$=\left\{−\mathrm{6},\:−\mathrm{1},\:\mathrm{1},\:\mathrm{6}\right\} \\ $$$$\mathrm{You}\:\mathrm{would}\:\mathrm{need}\:\mathrm{an}\:\mathrm{extra}\:\mathrm{rule}\:\mathrm{saying} \\ $$$$``\sqrt{{x}}\:\mathrm{is}\:\mathrm{always}\:\mathrm{positive}\:\mathrm{except}\:\mathrm{when}\:\mathrm{not} \\ $$$$\mathrm{used}\:\mathrm{in}\:\mathrm{any}\:\mathrm{calculation}''\:\mathrm{which}\:\mathrm{I}\:\mathrm{bet}\:\mathrm{you} \\ $$$$\mathrm{have}\:\mathrm{never}\:\mathrm{learned}\:\mathrm{before}. \\ $$
