
Question Number 184264 by Noorzai last updated on 04/Jan/23
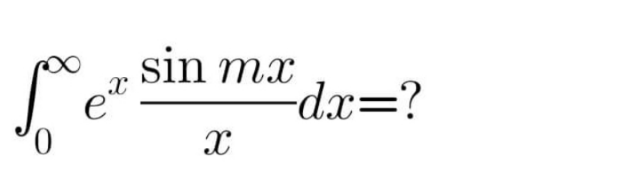
Answered by ARUNG_Brandon_MBU last updated on 04/Jan/23
![I(t)=∫_0 ^∞ e^(−tx) ((sinmx)/x)dx ⇒I′(t)=−∫_0 ^∞ e^(−tx) sinmxdx ⇒I′(t)=−[(e^(−tx) /(t^2 +m^2 ))(−tsinmx−mcosmx)]_0 ^∞ =−(m/(t^2 +m^2 )) ⇒I(t)=−arctan((t/m))+C lim_(t→+∞) I(t)=0=−(π/2)+C ⇒C=(π/2) ⇒I(t)=(π/2)−arctan((t/m)) ⇒∫_0 ^∞ e^x ((sinmx)/x)dx=I(−1)=(π/2)+arctan((1/m))](Q184267.png)
$${I}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} \frac{\mathrm{sin}{mx}}{{x}}{dx}\:\Rightarrow{I}'\left({t}\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} \mathrm{sin}{mxdx} \\ $$$$\Rightarrow{I}'\left({t}\right)=−\left[\frac{{e}^{−{tx}} }{{t}^{\mathrm{2}} +{m}^{\mathrm{2}} }\left(−{t}\mathrm{sin}{mx}−{m}\mathrm{cos}{mx}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{{m}}{{t}^{\mathrm{2}} +{m}^{\mathrm{2}} }\:\Rightarrow{I}\left({t}\right)=−\mathrm{arctan}\left(\frac{{t}}{{m}}\right)+{C} \\ $$$$\underset{{t}\rightarrow+\infty} {\mathrm{lim}}{I}\left({t}\right)=\mathrm{0}=−\frac{\pi}{\mathrm{2}}+{C}\:\Rightarrow{C}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{I}\left({t}\right)=\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\frac{{t}}{{m}}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} {e}^{{x}} \frac{\mathrm{sin}{mx}}{{x}}{dx}={I}\left(−\mathrm{1}\right)=\frac{\pi}{\mathrm{2}}+\mathrm{arctan}\left(\frac{\mathrm{1}}{{m}}\right) \\ $$
