
Question Number 184144 by paul2222 last updated on 03/Jan/23
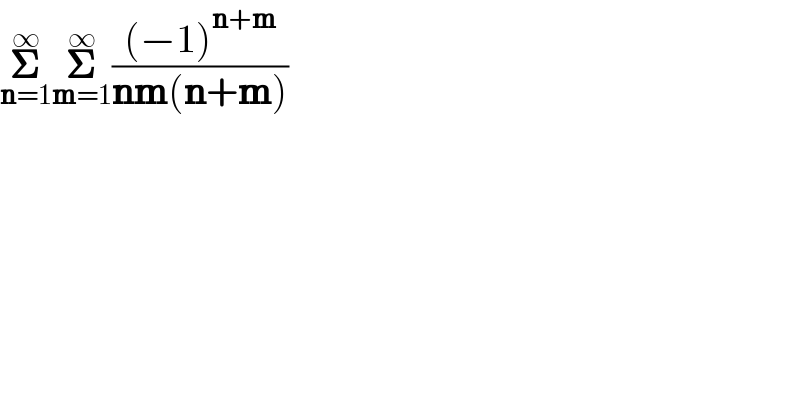
$$\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\underset{\boldsymbol{\mathrm{m}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{m}}} }{\boldsymbol{\mathrm{nm}}\left(\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{m}}\right)} \\ $$
Answered by SEKRET last updated on 04/Jan/23

$$\:\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\centerdot\underset{\boldsymbol{\mathrm{m}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{m}}} }{\boldsymbol{\mathrm{m}}\centerdot\left(\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{m}}\right)} \\ $$$$\:\:\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)_{\boldsymbol{\mathrm{x}}=−\mathrm{1}} \:\:=\:\underset{\boldsymbol{\mathrm{m}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{m}}} }{\boldsymbol{\mathrm{m}}\centerdot\left(\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{m}}\right)} \\ $$$$\:\:\:\boldsymbol{\mathrm{f}}\:'\:\left(\boldsymbol{\mathrm{x}}\right)\:=\:\underset{\boldsymbol{\mathrm{m}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{m}}−\mathrm{1}} }{\boldsymbol{\mathrm{m}}}=\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}−\mathrm{1}} \centerdot\underset{\boldsymbol{\mathrm{m}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{m}}} }{\boldsymbol{\mathrm{m}}} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{f}}\:'\:\left(\boldsymbol{\mathrm{x}}\right)\:=\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}−\mathrm{1}} \:\centerdot\:\boldsymbol{\mathrm{ln}}\left(\frac{\mathrm{1}}{\mathrm{1}−\boldsymbol{\mathrm{x}}}\right)\:\:\:\:\:\:\boldsymbol{\mathrm{C}}=\mathrm{0} \\ $$$$\:\:\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{−\mathrm{1}}{\boldsymbol{\mathrm{n}}}\centerdot\left(\int\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}−\mathrm{1}} \centerdot\boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{dx}}\right)\right)_{\boldsymbol{\mathrm{x}}=−\mathrm{1}} ^{\:\:\:\boldsymbol{\mathrm{C}}=\mathrm{0}} \\ $$$$\:\:\:\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(−\:\frac{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}} \centerdot\boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)\:+\boldsymbol{\mathrm{B}}_{\boldsymbol{\mathrm{x}}} \left(\boldsymbol{\mathrm{n}}+\mathrm{1},\mathrm{0}\right)}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\:\right) \\ $$$$\:\:\:\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{−\left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}} \centerdot\boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right)}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\:−\:\frac{\boldsymbol{\mathrm{B}}_{−\mathrm{1}} \left(\boldsymbol{\mathrm{n}}+\mathrm{1}\:;\:\mathrm{0}\right)}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right)= \\ $$$$\:\:=−\mathrm{1}\centerdot\boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right)\centerdot\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}} }{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\:+\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{−\boldsymbol{\mathrm{B}}_{−\mathrm{1}} \left(\boldsymbol{\mathrm{n}}+\mathrm{1},\mathrm{0}\right)}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }= \\ $$$$=\:\frac{\boldsymbol{\pi}^{\mathrm{2}} \centerdot\boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right)}{\mathrm{12}}\:+\:\left(\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \boldsymbol{\Psi}^{\mathrm{0}} \left(\frac{\boldsymbol{\mathrm{n}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\:+\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{−\boldsymbol{\Psi}^{\mathrm{0}} \left(\frac{\boldsymbol{\mathrm{n}}}{\mathrm{2}}+\mathrm{1}\right)}{\mathrm{2}\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right) \\ $$$$=\:\frac{\boldsymbol{\pi}^{\mathrm{2}} \centerdot\boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right)}{\mathrm{12}}\:+\left(\:−\mathrm{0}.\mathrm{28159}\:−\mathrm{0}.\mathrm{337683}\right) \\ $$$$\:\:\approx\:\mathrm{0}.\mathrm{0491823} \\ $$$$\boldsymbol{{ABDULAZIZ}}\:\:\boldsymbol{{ABDUVALIYEV}} \\ $$$$\:\:\:\:\:\: \\ $$
Commented by paul2222 last updated on 11/Jan/23

$$ \\ $$
Answered by witcher3 last updated on 05/Jan/23
![∫_0 ^1 ((ln^2 (1+x))/x)dx=−li_2 (−x)ln(1+x)+∫_0 ^1 ((li_2 (−x))/(1+x))dx....(E) Li_2 (−x)=ζ(2)−ln(1+x)ln(−x)−li_2 (1+x) =li_2 (−x)ln(1+x)−Li_3 (1+x)+ζ(2)ln(1+x) −∫_0 ^1 ((ln(1+x))/(1+x))ln(−x) =−(1/2)ln^2 (1+x)ln(−x)+(1/2)∫((ln^2 (1+x))/x)dx =−2li_2 (−x)ln(1+x)−2Li_3 (1+x)+2ζ(2)ln(1+x)−ln^2 (1+x)ln(−x) li_2 (−x)=ζ(2)−ln(−x)ln(1+x)−li_2 (1+x) ∫((ln^2 (1+x))/x)dx=−2li_3 (1+x)+2li_2 (1+x)ln(1+x)+ln^2 (1+x)ln(−x)+c Let f(x)=Σ_(n≥1) Σ_(m≥1) (((−1)^(n+m) x^(n+m) )/(nm(n+m))),∀x∈[−1,1] f′(x)=ΣΣ(((−1)^(n+m) )/(nm))x^(n+m−1) =(1/x)ΣΣ(((−x)^n (−x)^m )/(n.m)) =(1/x){Σ(((−x)^n )/n)}{Σ(((−x)^m )/m)} Σ_(n≥1) (((−1)^(n−1) x^n )/n)=ln(1+x) f^′ (x)=((ln^(2() (1+x))/x) f(x)=∫((ln^2 (1+x))/x)dx...(E) apply f(x)=−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+c f(0)=0 lim_(x→0) {−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+c}=0 ⇔c−2ζ(3)=0 c=2ζ(3) f(x)=−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+2ζ(3) our Sum=f(1)](Q184343.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{{x}}{dx}=−{li}_{\mathrm{2}} \left(−{x}\right){ln}\left(\mathrm{1}+{x}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{li}_{\mathrm{2}} \left(−{x}\right)}{\mathrm{1}+{x}}{dx}....\left({E}\right) \\ $$$${Li}_{\mathrm{2}} \left(−{x}\right)=\zeta\left(\mathrm{2}\right)−{ln}\left(\mathrm{1}+{x}\right){ln}\left(−{x}\right)−{li}_{\mathrm{2}} \left(\mathrm{1}+{x}\right) \\ $$$$={li}_{\mathrm{2}} \left(−{x}\right){ln}\left(\mathrm{1}+{x}\right)−{Li}_{\mathrm{3}} \left(\mathrm{1}+{x}\right)+\zeta\left(\mathrm{2}\right){ln}\left(\mathrm{1}+{x}\right) \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}{ln}\left(−{x}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right){ln}\left(−{x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$$$=−\mathrm{2}{li}_{\mathrm{2}} \left(−{x}\right){ln}\left(\mathrm{1}+{x}\right)−\mathrm{2}{Li}_{\mathrm{3}} \left(\mathrm{1}+{x}\right)+\mathrm{2}\zeta\left(\mathrm{2}\right){ln}\left(\mathrm{1}+{x}\right)−{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right){ln}\left(−{x}\right) \\ $$$${li}_{\mathrm{2}} \left(−{x}\right)=\zeta\left(\mathrm{2}\right)−{ln}\left(−{x}\right){ln}\left(\mathrm{1}+{x}\right)−{li}_{\mathrm{2}} \left(\mathrm{1}+{x}\right) \\ $$$$\int\frac{{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{{x}}{dx}=−\mathrm{2}{li}_{\mathrm{3}} \left(\mathrm{1}+{x}\right)+\mathrm{2}{li}_{\mathrm{2}} \left(\mathrm{1}+{x}\right){ln}\left(\mathrm{1}+{x}\right)+{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right){ln}\left(−{x}\right)+{c} \\ $$$${Let}\:{f}\left({x}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}+{m}} {x}^{{n}+{m}} }{{nm}\left({n}+{m}\right)},\forall{x}\in\left[−\mathrm{1},\mathrm{1}\right] \\ $$$${f}'\left({x}\right)=\Sigma\Sigma\frac{\left(−\mathrm{1}\right)^{{n}+{m}} }{{nm}}{x}^{{n}+{m}−\mathrm{1}} =\frac{\mathrm{1}}{{x}}\Sigma\Sigma\frac{\left(−{x}\right)^{{n}} \left(−{x}\right)^{{m}} }{{n}.{m}} \\ $$$$=\frac{\mathrm{1}}{{x}}\left\{\Sigma\frac{\left(−{x}\right)^{{n}} }{{n}}\right\}\left\{\Sigma\frac{\left(−{x}\right)^{{m}} }{{m}}\right\} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}^{{n}} }{{n}}={ln}\left(\mathrm{1}+{x}\right) \\ $$$${f}^{'} \left({x}\right)=\frac{{ln}^{\mathrm{2}\left(\right.} \left(\mathrm{1}+{x}\right)}{{x}} \\ $$$${f}\left({x}\right)=\int\frac{{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{{x}}{dx}...\left({E}\right)\:{apply}\: \\ $$$${f}\left({x}\right)=−\mathrm{2}{Li}_{\mathrm{3}} \left(\mathrm{1}+{x}\right)+\mathrm{2}{Li}_{\mathrm{2}} \left(\mathrm{1}+{x}\right){ln}\left(\mathrm{1}+{x}\right)+{ln}\left(−{x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)+{c} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{−\mathrm{2}{Li}_{\mathrm{3}} \left(\mathrm{1}+{x}\right)+\mathrm{2}{Li}_{\mathrm{2}} \left(\mathrm{1}+{x}\right){ln}\left(\mathrm{1}+{x}\right)+{ln}\left(−{x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)+{c}\right\}=\mathrm{0} \\ $$$$\Leftrightarrow{c}−\mathrm{2}\zeta\left(\mathrm{3}\right)=\mathrm{0} \\ $$$${c}=\mathrm{2}\zeta\left(\mathrm{3}\right) \\ $$$$ \\ $$$${f}\left({x}\right)=−\mathrm{2}{Li}_{\mathrm{3}} \left(\mathrm{1}+{x}\right)+\mathrm{2}{Li}_{\mathrm{2}} \left(\mathrm{1}+{x}\right){ln}\left(\mathrm{1}+{x}\right)+{ln}\left(−{x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)+\mathrm{2}\zeta\left(\mathrm{3}\right) \\ $$$${our}\:{Sum}={f}\left(\mathrm{1}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
