
Question Number 184091 by Ib last updated on 02/Jan/23

Commented by Ib last updated on 02/Jan/23

$${j}\:{ai}\:{besoin}\:{d}\:{aide} \\ $$$$ \\ $$$$ \\ $$
Answered by CElcedricjunior last updated on 02/Jan/23

$${A}=\left(\mathrm{2}\boldsymbol{{x}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\sqrt[{\mathrm{2}}]{\left(\mathrm{2}\boldsymbol{{x}}\right)^{\mathrm{3}} } \\ $$$$\boldsymbol{{A}}^{\mathrm{2}} =\mathrm{8}\boldsymbol{{x}}^{\mathrm{3}} \\ $$$$\boldsymbol{{B}}=\left(\mathrm{2}{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\left(\mathrm{2}{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{2}\left(\mathrm{2}\boldsymbol{{x}}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{\mathrm{8}\boldsymbol{{x}}^{\mathrm{3}} } \\ $$$$=>\boldsymbol{{B}}^{\mathrm{2}} =\mathrm{8}\boldsymbol{{x}}^{\mathrm{3}} \\ $$$$<=>\boldsymbol{{A}}^{\mathrm{2}} −\boldsymbol{{B}}^{\mathrm{2}} =\mathrm{8}{x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{3}} =\mathrm{0} \\ $$$$=>\boldsymbol{{A}}^{\mathrm{2}} =\boldsymbol{{B}}^{\mathrm{2}} =>{A}=\boldsymbol{{B}} \\ $$$$\left.\mathrm{2}\right)\left(\mathrm{1}+\frac{\boldsymbol{{t}}}{\mathrm{100}}\right)^{\mathrm{10}} =\mathrm{3}=>\frac{\boldsymbol{{t}}}{\mathrm{100}}<<<<\mathrm{1} \\ $$$$=>\left(\mathrm{1}+\frac{\boldsymbol{{t}}}{\mathrm{100}}\right)^{\mathrm{10}} =\mathrm{3}\:\:\boldsymbol{{or}}\:\left(\mathrm{1}+\boldsymbol{{a}}\right)^{\boldsymbol{{n}}} =\mathrm{1}+\boldsymbol{{na}}\:\boldsymbol{{pour}}\:\boldsymbol{{a}}<<\mathrm{1} \\ $$$$=>\mathrm{1}+\frac{\mathrm{10}\boldsymbol{{t}}}{\mathrm{100}}=\mathrm{3} \\ $$$$=>\frac{\boldsymbol{{t}}}{\mathrm{10}}=\mathrm{2}=>\boldsymbol{{t}}=\mathrm{20} \\ $$$$========================== \\ $$$$......................{le}\:{celebre}\:{cedric}\:{junior}........ \\ $$$$======================== \\ $$$$\boldsymbol{{y}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{ae}}^{−\mathrm{6}\boldsymbol{{x}}} +\boldsymbol{{be}}^{−\mathrm{2}\boldsymbol{{x}}} +\boldsymbol{{c}}\:\: \\ $$$$\boldsymbol{{a}};\boldsymbol{{bet}}\:\boldsymbol{{c}}\in\mathbb{R} \\ $$$$ \\ $$
Answered by manxsol last updated on 02/Jan/23
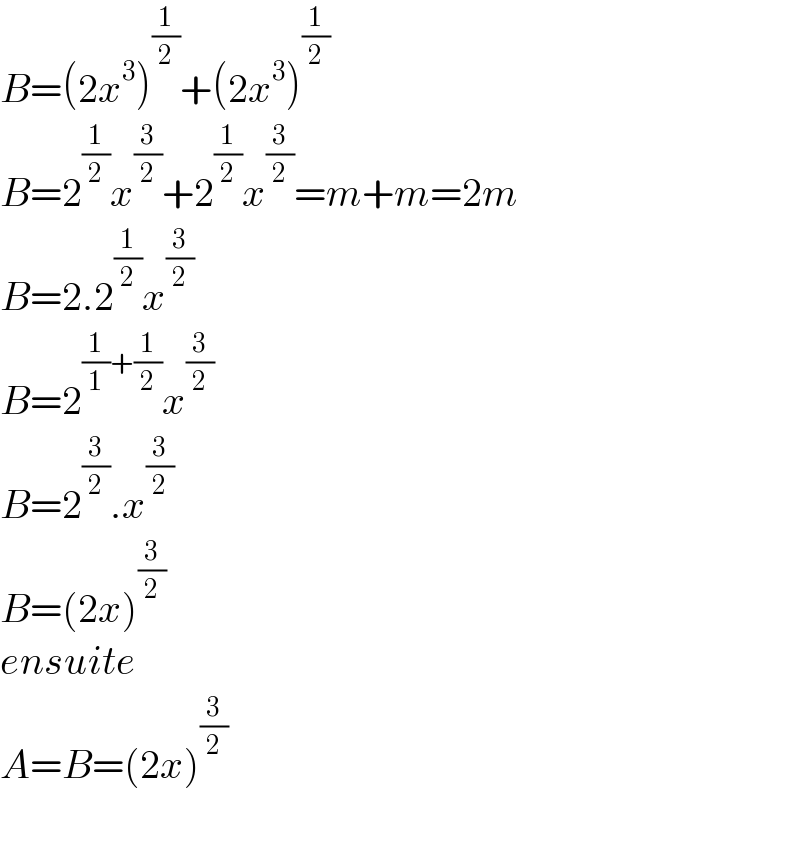
$${B}=\left(\mathrm{2}{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\left(\mathrm{2}{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${B}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{3}}{\mathrm{2}}} ={m}+{m}=\mathrm{2}{m} \\ $$$${B}=\mathrm{2}.\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${B}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${B}=\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} .{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${B}=\left(\mathrm{2}{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${ensuite} \\ $$$${A}={B}=\left(\mathrm{2}{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$ \\ $$
