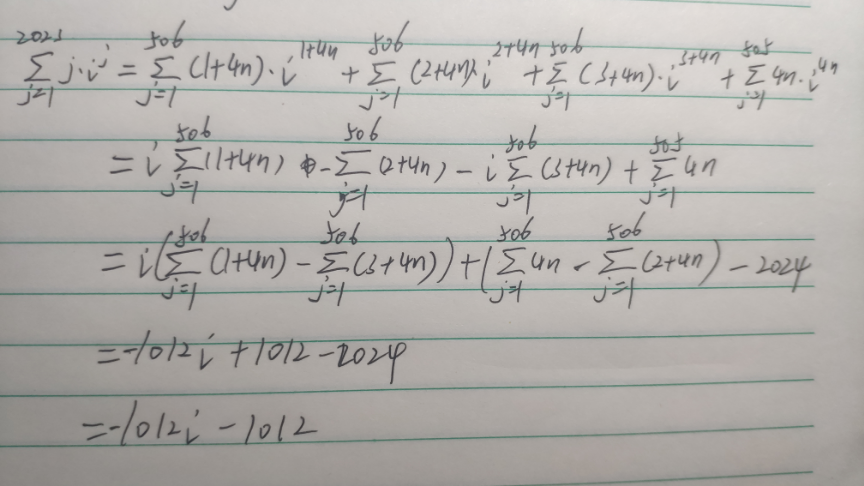Question Number 184037 by liuxinnan last updated on 02/Jan/23

$${i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$\underset{{j}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}{ji}^{{j}} =? \\ $$
Answered by SEKRET last updated on 02/Jan/23
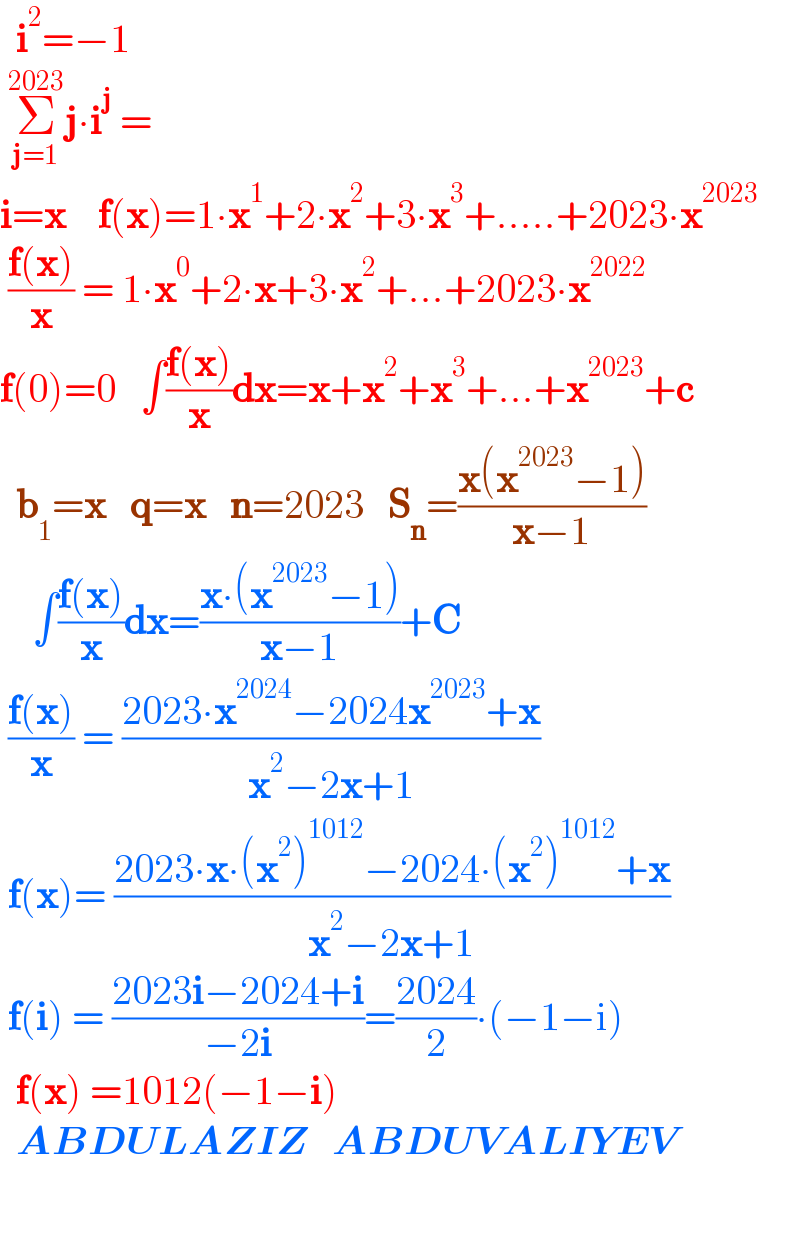
$$\:\:\boldsymbol{\mathrm{i}}^{\mathrm{2}} =−\mathrm{1}\:\:\: \\ $$$$\:\underset{\boldsymbol{\mathrm{j}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\boldsymbol{\mathrm{j}}\centerdot\boldsymbol{\mathrm{i}}^{\boldsymbol{\mathrm{j}}} \:= \\ $$$$\boldsymbol{\mathrm{i}}=\boldsymbol{\mathrm{x}}\:\:\:\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{1}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{1}} +\mathrm{2}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{3}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{3}} +.....+\mathrm{2023}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{2023}} \\ $$$$\:\frac{\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}}\:=\:\mathrm{1}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{0}} +\mathrm{2}\centerdot\boldsymbol{\mathrm{x}}+\mathrm{3}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{2}} +...+\mathrm{2023}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{2022}} \\ $$$$\boldsymbol{\mathrm{f}}\left(\mathrm{0}\right)=\mathrm{0}\:\:\:\int\frac{\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}}=\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}^{\mathrm{3}} +...+\boldsymbol{\mathrm{x}}^{\mathrm{2023}} +\boldsymbol{\mathrm{c}} \\ $$$$\:\:\boldsymbol{\mathrm{b}}_{\mathrm{1}} =\boldsymbol{\mathrm{x}}\:\:\:\boldsymbol{\mathrm{q}}=\boldsymbol{\mathrm{x}}\:\:\:\boldsymbol{\mathrm{n}}=\mathrm{2023}\:\:\:\boldsymbol{\mathrm{S}}_{\boldsymbol{\mathrm{n}}} =\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2023}} −\mathrm{1}\right)}{\boldsymbol{\mathrm{x}}−\mathrm{1}} \\ $$$$\:\:\:\:\int\frac{\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}}=\frac{\boldsymbol{\mathrm{x}}\centerdot\left(\boldsymbol{\mathrm{x}}^{\mathrm{2023}} −\mathrm{1}\right)}{\boldsymbol{\mathrm{x}}−\mathrm{1}}+\boldsymbol{\mathrm{C}} \\ $$$$\:\frac{\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}}\:=\:\frac{\mathrm{2023}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{2024}} −\mathrm{2024}\boldsymbol{\mathrm{x}}^{\mathrm{2023}} +\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{1}} \\ $$$$\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\:\frac{\mathrm{2023}\centerdot\boldsymbol{\mathrm{x}}\centerdot\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)^{\mathrm{1012}} −\mathrm{2024}\centerdot\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)^{\mathrm{1012}} +\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{1}} \\ $$$$\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{i}}\right)\:=\:\frac{\mathrm{2023}\boldsymbol{\mathrm{i}}−\mathrm{2024}+\boldsymbol{\mathrm{i}}}{−\mathrm{2}\boldsymbol{\mathrm{i}}}=\frac{\mathrm{2024}}{\mathrm{2}}\centerdot\left(−\mathrm{1}−\mathrm{i}\right) \\ $$$$\:\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\:=\mathrm{1012}\left(−\mathrm{1}−\boldsymbol{\mathrm{i}}\right) \\ $$$$\:\:\boldsymbol{{ABDULAZIZ}}\:\:\:\boldsymbol{{ABDUVALIYEV}} \\ $$$$ \\ $$
Answered by liuxinnan last updated on 02/Jan/23