
Question Number 183998 by JDamian last updated on 01/Jan/23
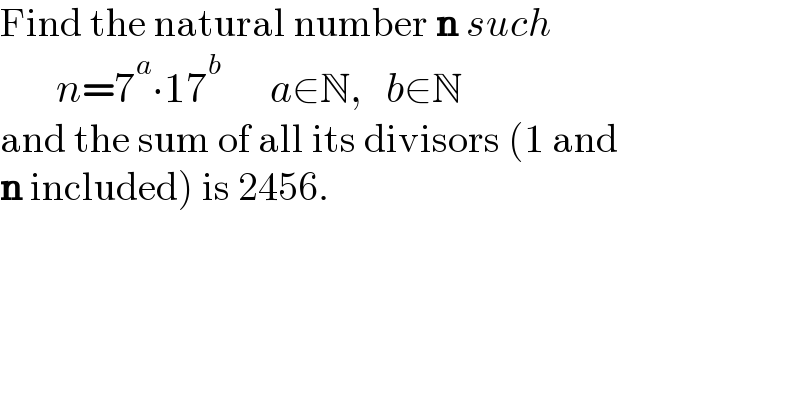
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{natural}\:\mathrm{number}\:\boldsymbol{\mathrm{n}}\:{such} \\ $$$$\:\:\:\:\:\:\:{n}=\mathrm{7}^{{a}} \centerdot\mathrm{17}^{{b}} \:\:\:\:\:\:{a}\in\mathbb{N},\:\:\:{b}\in\mathbb{N} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{its}\:\mathrm{divisors}\:\left(\mathrm{1}\:\mathrm{and}\right. \\ $$$$\left.\boldsymbol{\mathrm{n}}\:\mathrm{included}\right)\:\mathrm{is}\:\mathrm{2456}. \\ $$
Commented by Rasheed.Sindhi last updated on 01/Jan/23

$$\:\:\:\:\:\:\:\:\:\begin{array}{|c|}{\boldsymbol{\mathrm{n}}=\mathrm{2023}=\mathrm{7}^{\mathrm{1}} \centerdot\mathrm{17}^{\mathrm{2}} }\\\hline\end{array} \\ $$$$\underset{−} {\overline {\bigstar_{\bigstar} ^{\bigstar} \boldsymbol{\mathrm{Happy}}\:\boldsymbol{\mathrm{New}}\:\boldsymbol{\mathrm{Year}}_{\bigstar} ^{\bigstar} \bigstar}} \\ $$
Answered by Rasheed.Sindhi last updated on 01/Jan/23

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\begin{array}{|c|}{\underset{\underset{\underset{=\mathrm{2456}} {\mathrm{1}+\mathrm{7}+\mathrm{17}+\mathrm{119}+\mathrm{289}+\mathrm{2023}}} {\:\boldsymbol{\mathcal{S}{um}\mathcal{O}{f}\mathcal{D}}{ivisors}}} {\boldsymbol{\mathrm{n}}=\mathrm{2023}=\mathrm{7}^{\mathrm{1}} \centerdot\mathrm{17}^{\mathrm{2}} }}\\\hline\end{array} \\ $$$$ \\ $$
