
Question Number 183846 by Michaelfaraday last updated on 30/Dec/22
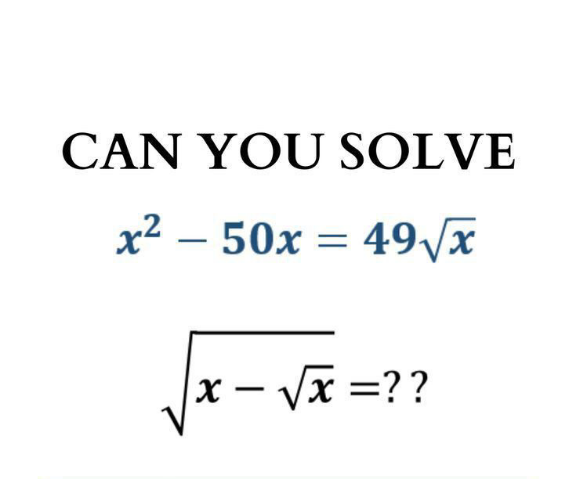
Answered by MJS_new last updated on 31/Dec/22
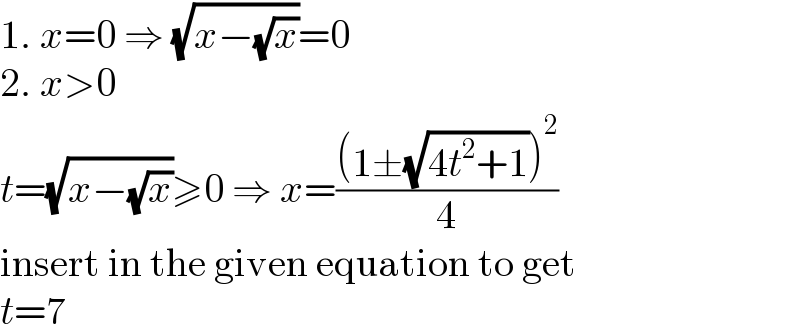
$$\mathrm{1}.\:{x}=\mathrm{0}\:\Rightarrow\:\sqrt{{x}−\sqrt{{x}}}=\mathrm{0} \\ $$$$\mathrm{2}.\:{x}>\mathrm{0} \\ $$$${t}=\sqrt{{x}−\sqrt{{x}}}\geqslant\mathrm{0}\:\Rightarrow\:{x}=\frac{\left(\mathrm{1}\pm\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{to}\:\mathrm{get} \\ $$$${t}=\mathrm{7} \\ $$
Commented by Michaelfaraday last updated on 31/Dec/22
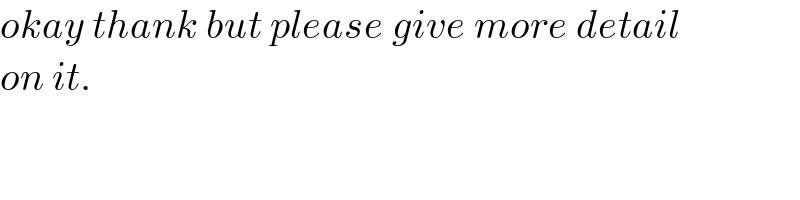
$${okay}\:{thank}\:{but}\:{please}\:{give}\:{more}\:{detail} \\ $$$${on}\:{it}. \\ $$
Commented by MJS_new last updated on 31/Dec/22

$$\mathrm{I}\:\mathrm{give}\:\mathrm{the}\:\mathrm{path}\:\mathrm{you}\:\mathrm{do}\:\mathrm{the}\:\mathrm{writing}\:\mathrm{work}.\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{easy}... \\ $$
Commented by Michaelfaraday last updated on 31/Dec/22

$${okay}\:{sir} \\ $$
Answered by mr W last updated on 31/Dec/22
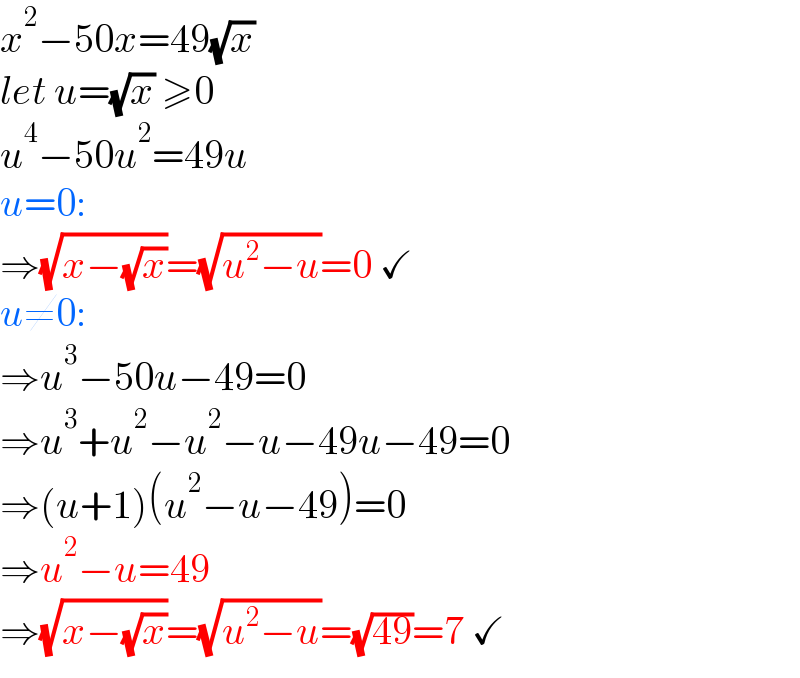
$${x}^{\mathrm{2}} −\mathrm{50}{x}=\mathrm{49}\sqrt{{x}} \\ $$$${let}\:{u}=\sqrt{{x}}\:\geqslant\mathrm{0} \\ $$$${u}^{\mathrm{4}} −\mathrm{50}{u}^{\mathrm{2}} =\mathrm{49}{u} \\ $$$${u}=\mathrm{0}: \\ $$$$\Rightarrow\sqrt{{x}−\sqrt{{x}}}=\sqrt{{u}^{\mathrm{2}} −{u}}=\mathrm{0}\:\checkmark \\ $$$${u}\neq\mathrm{0}: \\ $$$$\Rightarrow{u}^{\mathrm{3}} −\mathrm{50}{u}−\mathrm{49}=\mathrm{0} \\ $$$$\Rightarrow{u}^{\mathrm{3}} +{u}^{\mathrm{2}} −{u}^{\mathrm{2}} −{u}−\mathrm{49}{u}−\mathrm{49}=\mathrm{0} \\ $$$$\Rightarrow\left({u}+\mathrm{1}\right)\left({u}^{\mathrm{2}} −{u}−\mathrm{49}\right)=\mathrm{0} \\ $$$$\Rightarrow{u}^{\mathrm{2}} −{u}=\mathrm{49}\: \\ $$$$\Rightarrow\sqrt{{x}−\sqrt{{x}}}=\sqrt{{u}^{\mathrm{2}} −{u}}=\sqrt{\mathrm{49}}=\mathrm{7}\:\checkmark \\ $$
Commented by Michaelfaraday last updated on 31/Dec/22

$${thanks}\:{sir} \\ $$
Answered by manxsol last updated on 31/Dec/22
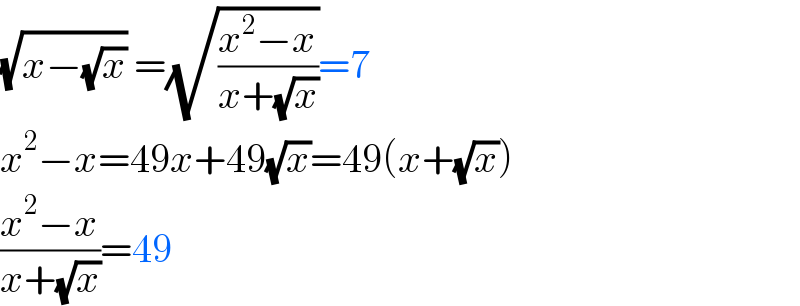
$$\sqrt{{x}−\sqrt{{x}}}\:=\sqrt{\frac{{x}^{\mathrm{2}} −{x}}{{x}+\sqrt{{x}}}}=\mathrm{7} \\ $$$${x}^{\mathrm{2}} −{x}=\mathrm{49}{x}+\mathrm{49}\sqrt{{x}}=\mathrm{49}\left({x}+\sqrt{{x}}\right) \\ $$$$\frac{{x}^{\mathrm{2}} −{x}}{{x}+\sqrt{{x}}}=\mathrm{49} \\ $$
Commented by Michaelfaraday last updated on 31/Dec/22

$${thanks}\:{sir} \\ $$
Answered by CElcedricjunior last updated on 31/Dec/22

$$\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{50}\boldsymbol{{x}}−\mathrm{49}\sqrt{\boldsymbol{{x}}}=\mathrm{0} \\ $$$$\boldsymbol{{posons}}\:\boldsymbol{{t}}=\sqrt{\boldsymbol{{x}}} \\ $$$$=>\boldsymbol{{t}}^{\mathrm{4}} −\mathrm{50}\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{49}\boldsymbol{{t}}=\mathrm{0} \\ $$$$=>\boldsymbol{{t}}=\mathrm{0}\boldsymbol{{ou}} \\ $$$$\boldsymbol{{t}}^{\mathrm{3}} −\mathrm{50}\boldsymbol{{t}}−\mathrm{49}=\mathrm{0} \\ $$$$\left(\boldsymbol{{t}}+\mathrm{1}\right)\left(\boldsymbol{{t}}^{\mathrm{2}} −\boldsymbol{{t}}−\mathrm{49}\right)=\mathrm{0} \\ $$$$\boldsymbol{{t}}=−\mathrm{1}\:\boldsymbol{{ou}}\:\boldsymbol{{t}}^{\mathrm{2}} −\boldsymbol{{t}}−\mathrm{49}=\mathrm{0} \\ $$$$\boldsymbol{\Delta}=\mathrm{1}+\mathrm{196}=\mathrm{197} \\ $$$$\boldsymbol{{t}}=\mathrm{0}\:\boldsymbol{{ou}}\:\boldsymbol{{t}}=−\mathrm{1}\:\boldsymbol{{ou}}\:\boldsymbol{{t}}=\frac{\mathrm{1}\mp\sqrt{\mathrm{197}}}{\mathrm{2}} \\ $$$$\boldsymbol{{t}}=\sqrt{\boldsymbol{{x}}}=>\boldsymbol{{x}}=\left(\frac{\mathrm{1}+\sqrt{\mathrm{197}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=> \\ $$$$\sqrt{\boldsymbol{{x}}−\sqrt{\boldsymbol{{x}}}}=\sqrt{\left(\frac{\mathrm{1}+\sqrt{\mathrm{197}}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{197}}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\mathrm{198}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{197}}−\mathrm{2}\sqrt{\mathrm{197}}}{\mathrm{4}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\mathrm{196}}{\mathrm{4}}}=\sqrt{\mathrm{49}}=\mathrm{7} \\ $$$$=>\sqrt{\boldsymbol{{x}}−\sqrt{\boldsymbol{{x}}}}=\mathrm{7} \\ $$$$======================== \\ $$$$............{le}\:{celebre}\:{cedric}\:{junior}........... \\ $$$$===================== \\ $$$$ \\ $$$$ \\ $$$$\left(\right. \\ $$
