
Question Number 183843 by Michaelfaraday last updated on 30/Dec/22

Answered by mr W last updated on 31/Dec/22
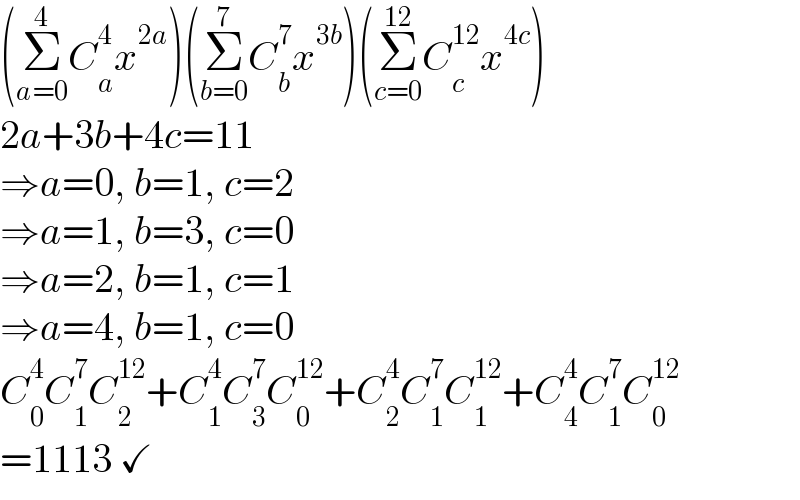
$$\left(\underset{{a}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}{C}_{{a}} ^{\mathrm{4}} {x}^{\mathrm{2}{a}} \right)\left(\underset{{b}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}{C}_{{b}} ^{\mathrm{7}} {x}^{\mathrm{3}{b}} \right)\left(\underset{{c}=\mathrm{0}} {\overset{\mathrm{12}} {\sum}}{C}_{{c}} ^{\mathrm{12}} {x}^{\mathrm{4}{c}} \right) \\ $$$$\mathrm{2}{a}+\mathrm{3}{b}+\mathrm{4}{c}=\mathrm{11} \\ $$$$\Rightarrow{a}=\mathrm{0},\:{b}=\mathrm{1},\:{c}=\mathrm{2} \\ $$$$\Rightarrow{a}=\mathrm{1},\:{b}=\mathrm{3},\:{c}=\mathrm{0} \\ $$$$\Rightarrow{a}=\mathrm{2},\:{b}=\mathrm{1},\:{c}=\mathrm{1} \\ $$$$\Rightarrow{a}=\mathrm{4},\:{b}=\mathrm{1},\:{c}=\mathrm{0} \\ $$$${C}_{\mathrm{0}} ^{\mathrm{4}} {C}_{\mathrm{1}} ^{\mathrm{7}} {C}_{\mathrm{2}} ^{\mathrm{12}} +{C}_{\mathrm{1}} ^{\mathrm{4}} {C}_{\mathrm{3}} ^{\mathrm{7}} {C}_{\mathrm{0}} ^{\mathrm{12}} +{C}_{\mathrm{2}} ^{\mathrm{4}} {C}_{\mathrm{1}} ^{\mathrm{7}} {C}_{\mathrm{1}} ^{\mathrm{12}} +{C}_{\mathrm{4}} ^{\mathrm{4}} {C}_{\mathrm{1}} ^{\mathrm{7}} {C}_{\mathrm{0}} ^{\mathrm{12}} \\ $$$$=\mathrm{1113}\:\checkmark \\ $$
Commented by manxsol last updated on 31/Dec/22
$${today}\:{learn},{thanks}\:{Sir}\:{W} \\ $$
Commented by Michaelfaraday last updated on 31/Dec/22

$${thanks} \\ $$
