
Question Number 183773 by HeferH last updated on 30/Dec/22
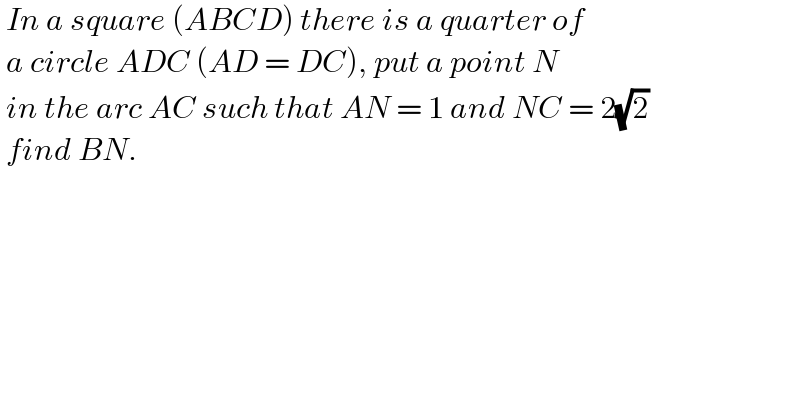
$$\:{In}\:{a}\:{square}\:\left({ABCD}\right)\:{there}\:{is}\:{a}\:{quarter}\:{of} \\ $$$$\:{a}\:{circle}\:{ADC}\:\left({AD}\:=\:{DC}\right),\:{put}\:{a}\:{point}\:{N} \\ $$$$\:{in}\:{the}\:{arc}\:{AC}\:{such}\:{that}\:{AN}\:=\:\mathrm{1}\:{and}\:{NC}\:=\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\:{find}\:{BN}.\: \\ $$$$\: \\ $$
Answered by mr W last updated on 30/Dec/22

Commented by mr W last updated on 30/Dec/22
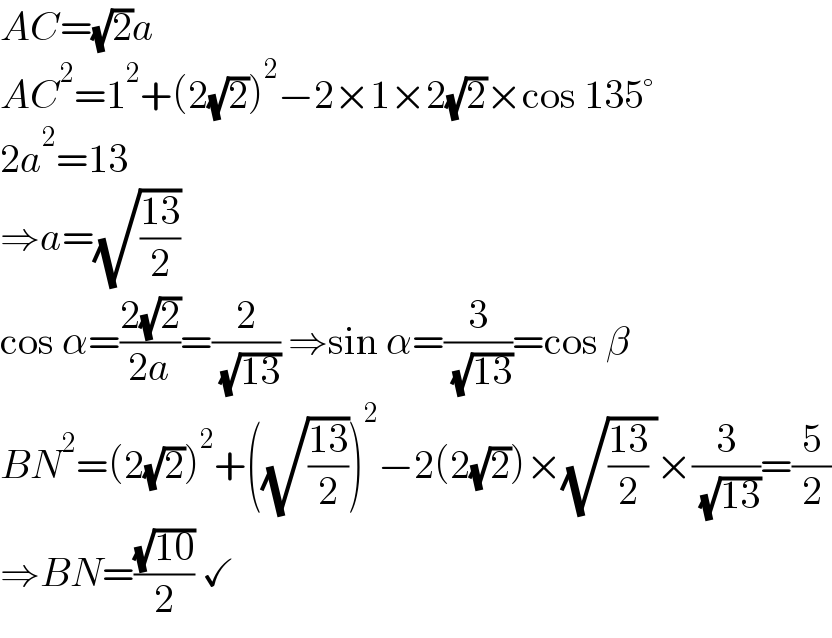
$${AC}=\sqrt{\mathrm{2}}{a} \\ $$$${AC}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×\mathrm{2}\sqrt{\mathrm{2}}×\mathrm{cos}\:\mathrm{135}° \\ $$$$\mathrm{2}{a}^{\mathrm{2}} =\mathrm{13} \\ $$$$\Rightarrow{a}=\sqrt{\frac{\mathrm{13}}{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}{a}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}\:\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}}=\mathrm{cos}\:\beta \\ $$$${BN}^{\mathrm{2}} =\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{13}}{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)×\sqrt{\frac{\mathrm{13}}{\mathrm{2}}\:}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow{BN}=\frac{\sqrt{\mathrm{10}}}{\mathrm{2}}\:\checkmark \\ $$
Answered by mr W last updated on 30/Dec/22
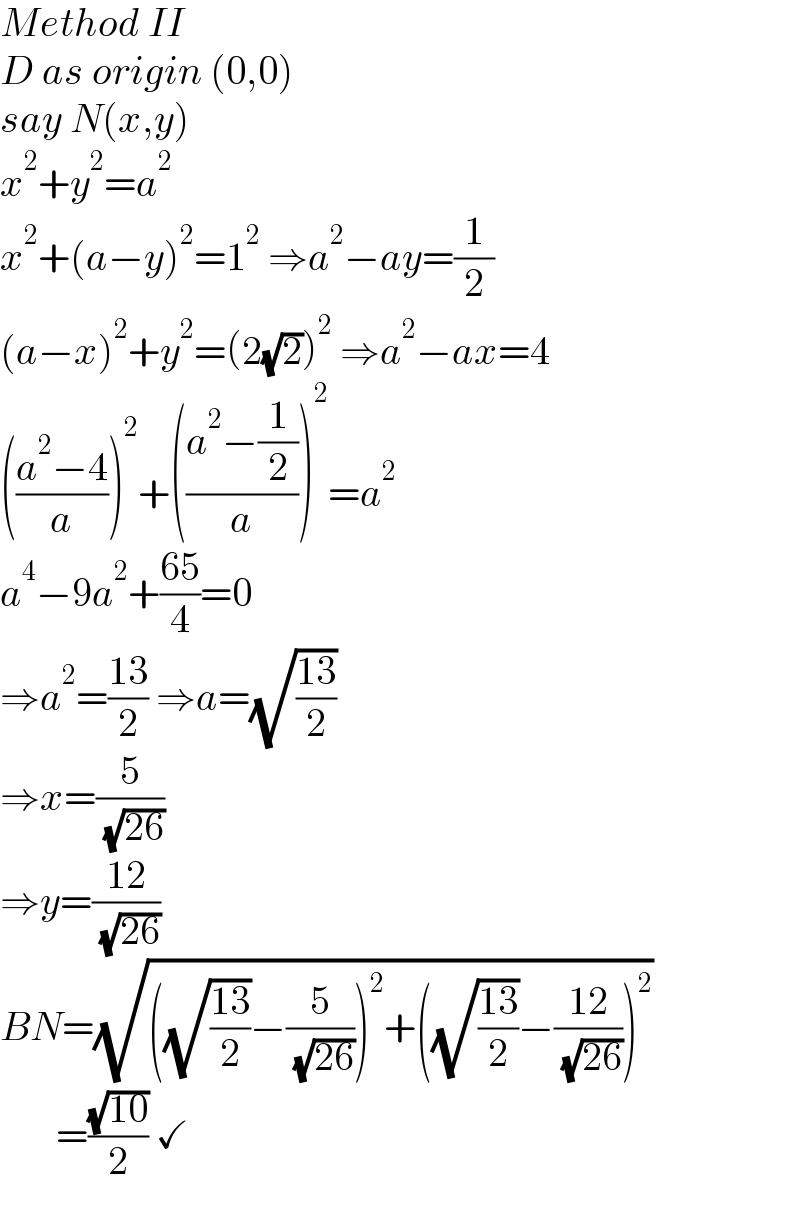
$${Method}\:{II} \\ $$$${D}\:{as}\:{origin}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$${say}\:{N}\left({x},{y}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \:\Rightarrow{a}^{\mathrm{2}} −{ay}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left({a}−{x}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:\Rightarrow{a}^{\mathrm{2}} −{ax}=\mathrm{4} \\ $$$$\left(\frac{{a}^{\mathrm{2}} −\mathrm{4}}{{a}}\right)^{\mathrm{2}} +\left(\frac{{a}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}}{{a}}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${a}^{\mathrm{4}} −\mathrm{9}{a}^{\mathrm{2}} +\frac{\mathrm{65}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{\mathrm{13}}{\mathrm{2}}\:\Rightarrow{a}=\sqrt{\frac{\mathrm{13}}{\mathrm{2}}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}}{\:\sqrt{\mathrm{26}}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{12}}{\:\sqrt{\mathrm{26}}} \\ $$$${BN}=\sqrt{\left(\sqrt{\frac{\mathrm{13}}{\mathrm{2}}}−\frac{\mathrm{5}}{\:\sqrt{\mathrm{26}}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{13}}{\mathrm{2}}}−\frac{\mathrm{12}}{\:\sqrt{\mathrm{26}}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{10}}}{\mathrm{2}}\:\checkmark \\ $$
