
Question Number 18369 by Tinkutara last updated on 19/Jul/17
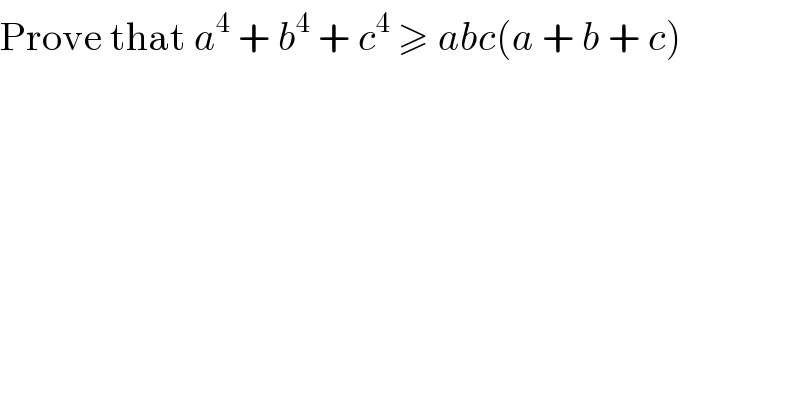
$$\mathrm{Prove}\:\mathrm{that}\:{a}^{\mathrm{4}} \:+\:{b}^{\mathrm{4}} \:+\:{c}^{\mathrm{4}} \:\geqslant\:{abc}\left({a}\:+\:{b}\:+\:{c}\right) \\ $$
Answered by mrW1 last updated on 19/Jul/17
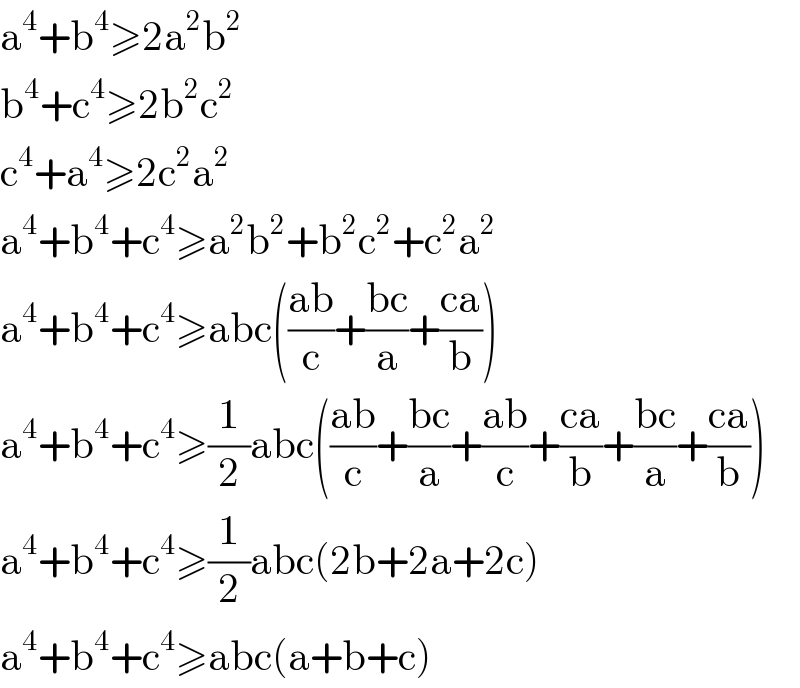
$$\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} \geqslant\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \\ $$$$\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \geqslant\mathrm{2b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} \\ $$$$\mathrm{c}^{\mathrm{4}} +\mathrm{a}^{\mathrm{4}} \geqslant\mathrm{2c}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \geqslant\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \geqslant\mathrm{abc}\left(\frac{\mathrm{ab}}{\mathrm{c}}+\frac{\mathrm{bc}}{\mathrm{a}}+\frac{\mathrm{ca}}{\mathrm{b}}\right) \\ $$$$\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \geqslant\frac{\mathrm{1}}{\mathrm{2}}\mathrm{abc}\left(\frac{\mathrm{ab}}{\mathrm{c}}+\frac{\mathrm{bc}}{\mathrm{a}}+\frac{\mathrm{ab}}{\mathrm{c}}+\frac{\mathrm{ca}}{\mathrm{b}}+\frac{\mathrm{bc}}{\mathrm{a}}+\frac{\mathrm{ca}}{\mathrm{b}}\right) \\ $$$$\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \geqslant\frac{\mathrm{1}}{\mathrm{2}}\mathrm{abc}\left(\mathrm{2b}+\mathrm{2a}+\mathrm{2c}\right) \\ $$$$\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \geqslant\mathrm{abc}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right) \\ $$
Commented by Tinkutara last updated on 19/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
