
Question Number 183664 by Rasheed.Sindhi last updated on 28/Dec/22
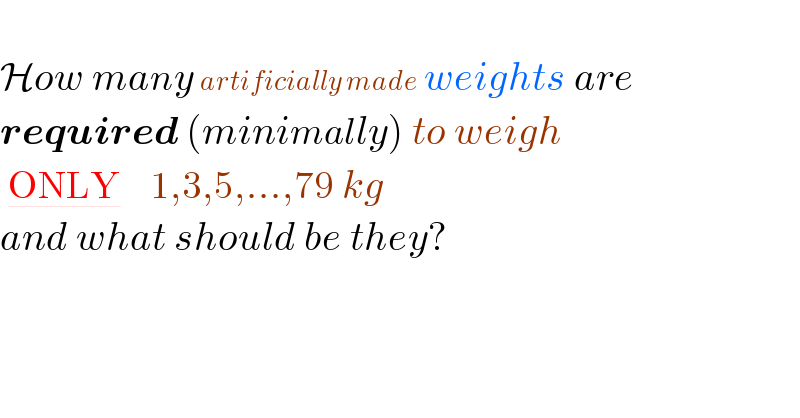
$$ \\ $$$$\mathcal{H}{ow}\:{many}\:{artificially}\:{made}\:{weights}\:{are}\: \\ $$$$\boldsymbol{{required}}\:\left({minimally}\right)\:{to}\:{weigh} \\ $$$$\:\underline{\mathrm{ONLY}}\:\:\:\:\:\mathrm{1},\mathrm{3},\mathrm{5},...,\mathrm{79}\:{kg}\: \\ $$$${and}\:{what}\:{should}\:{be}\:{they}? \\ $$
Commented by Frix last updated on 28/Dec/22
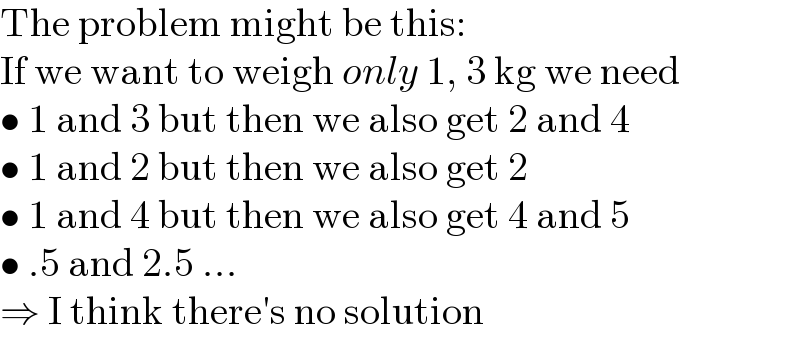
$$\mathrm{The}\:\mathrm{problem}\:\mathrm{might}\:\mathrm{be}\:\mathrm{this}: \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{want}\:\mathrm{to}\:\mathrm{weigh}\:{only}\:\mathrm{1},\:\mathrm{3}\:\mathrm{kg}\:\mathrm{we}\:\mathrm{need} \\ $$$$\bullet\:\mathrm{1}\:\mathrm{and}\:\mathrm{3}\:\mathrm{but}\:\mathrm{then}\:\mathrm{we}\:\mathrm{also}\:\mathrm{get}\:\mathrm{2}\:\mathrm{and}\:\mathrm{4} \\ $$$$\bullet\:\mathrm{1}\:\mathrm{and}\:\mathrm{2}\:\mathrm{but}\:\mathrm{then}\:\mathrm{we}\:\mathrm{also}\:\mathrm{get}\:\mathrm{2} \\ $$$$\bullet\:\mathrm{1}\:\mathrm{and}\:\mathrm{4}\:\mathrm{but}\:\mathrm{then}\:\mathrm{we}\:\mathrm{also}\:\mathrm{get}\:\mathrm{4}\:\mathrm{and}\:\mathrm{5} \\ $$$$\bullet\:.\mathrm{5}\:\mathrm{and}\:\mathrm{2}.\mathrm{5}\:... \\ $$$$\Rightarrow\:\mathrm{I}\:\mathrm{think}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{solution} \\ $$
Commented by Rasheed.Sindhi last updated on 29/Dec/22

$$\mathbb{T}\boldsymbol{\mathrm{han}}\mathbb{X}\:\mathrm{Frix}\:\mathrm{sir}!\:{very}\:{right}\:{are}\:{you}... \\ $$$${In}\:{case}\:{we}\:{release}\:{the}\:\underline{\mathrm{only}}\:{condition} \\ $$$${has}\:{the}\:{question}\:\:\mathrm{unique}\:{solution} \\ $$$${then}?\:{See}\:{Q}#\mathrm{183646} \\ $$
Commented by mr W last updated on 29/Dec/22

$${to}\:{weigh}\:{only}\:\mathrm{1},\mathrm{3},\mathrm{5},...,\mathrm{79}\:{kg},\:{there}\:{is} \\ $$$${no}\:{solution}. \\ $$$${to}\:{weigh}\:{not}\:{only}\:\mathrm{1},\mathrm{3},\mathrm{5},...,\mathrm{79}\:{kg},{we} \\ $$$${need}\:{at}\:{least}\:\mathrm{5}\:{weights}.\:{with}\:\mathrm{5}\:{weights} \\ $$$${there}\:{are}\:{at}\:{least}\:{two}\:{solutions}: \\ $$$$\mathrm{1},\mathrm{3},\mathrm{9},\mathrm{27},\mathrm{81}\:{or} \\ $$$$\mathrm{1},\mathrm{2},\mathrm{6},\mathrm{18},\mathrm{54}. \\ $$
Commented by Rasheed.Sindhi last updated on 29/Dec/22
$$\vee\:\cap\boldsymbol{\mathrm{i}}\subset\in\:\boldsymbol{\mathrm{sir}}!\:\:\mathcal{T}{han}\mathcal{X}! \\ $$
