
Question Number 183631 by a.lgnaoui last updated on 27/Dec/22
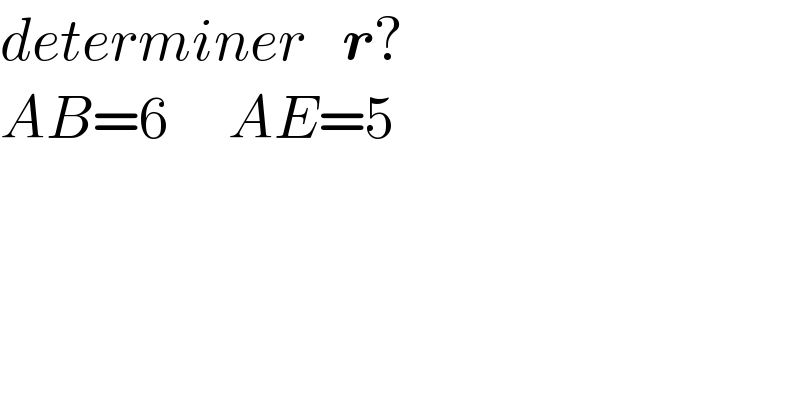
$${determiner}\:\:\:\boldsymbol{{r}}? \\ $$$${AB}=\mathrm{6}\:\:\:\:\:{AE}=\mathrm{5} \\ $$
Commented by a.lgnaoui last updated on 27/Dec/22
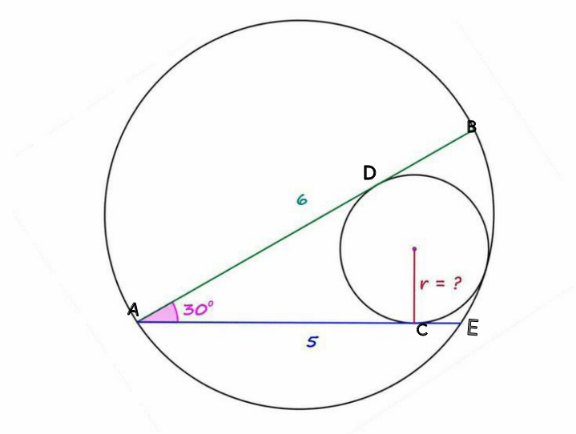
Answered by mr W last updated on 28/Dec/22
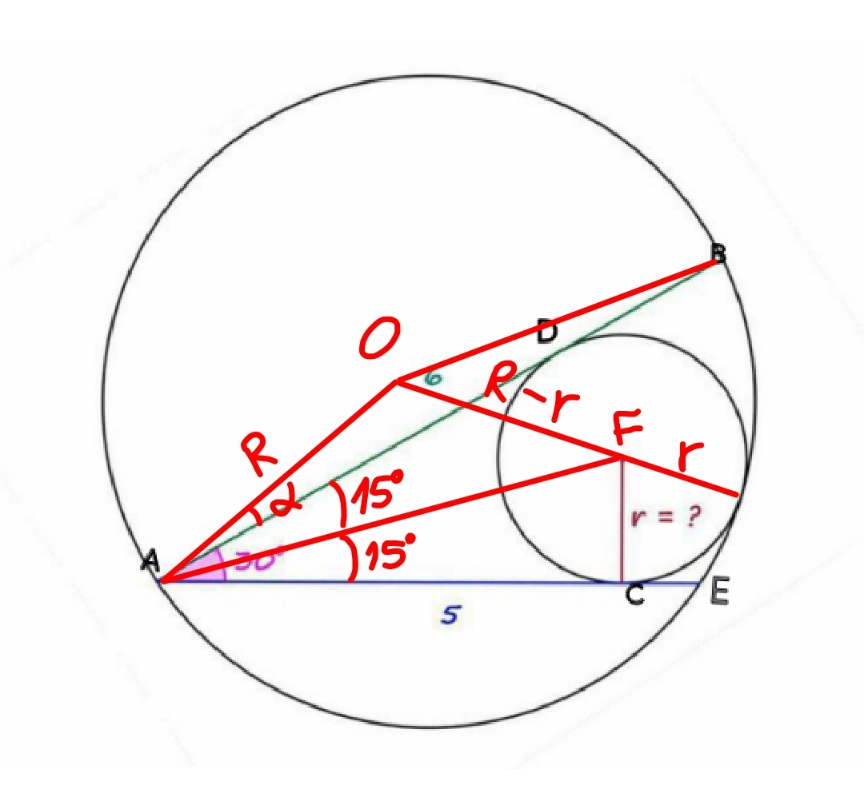
Commented by mr W last updated on 28/Dec/22

$${BE}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} −\mathrm{2}×\mathrm{5}×\mathrm{6}\:\mathrm{cos}\:\mathrm{30}° \\ $$$$\Rightarrow{BE}=\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}} \\ $$$${R}=\frac{\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{30}°}=\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{6}}{\mathrm{2}\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{52}−\mathrm{30}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}} \\ $$$${AF}=\frac{{r}}{\mathrm{sin}\:\mathrm{15}°}=\frac{\mathrm{4}{r}}{\:\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}=\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right){r} \\ $$$$\mathrm{cos}\:\left(\alpha+\mathrm{15}°\right)=\frac{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} \left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{2}{Rr}\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right)} \\ $$$$\mathrm{cos}\:\alpha\:\mathrm{cos}\:\mathrm{15}°−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\mathrm{15}°=\frac{\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right){r}+\mathrm{2}{R}}{\mathrm{2}{R}\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right)} \\ $$$$\frac{\mathrm{3}}{\:\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}}×\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}−\frac{\sqrt{\mathrm{52}−\mathrm{30}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}}×\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right){r}+\mathrm{2}{R}}{\mathrm{2}{R}\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right)} \\ $$$$\mathrm{3}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)−\sqrt{\mathrm{52}−\mathrm{30}\sqrt{\mathrm{3}}}=\frac{\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right){r}}{\mathrm{2}}+{R} \\ $$$$\Rightarrow{r}=\mathrm{2}\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)\left(\mathrm{6}+\mathrm{3}\sqrt{\mathrm{3}}−\sqrt{\mathrm{52}−\mathrm{30}\sqrt{\mathrm{3}}}−\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}\right)\approx\mathrm{1}.\mathrm{1478} \\ $$
