
Question Number 183592 by greougoury555 last updated on 27/Dec/22
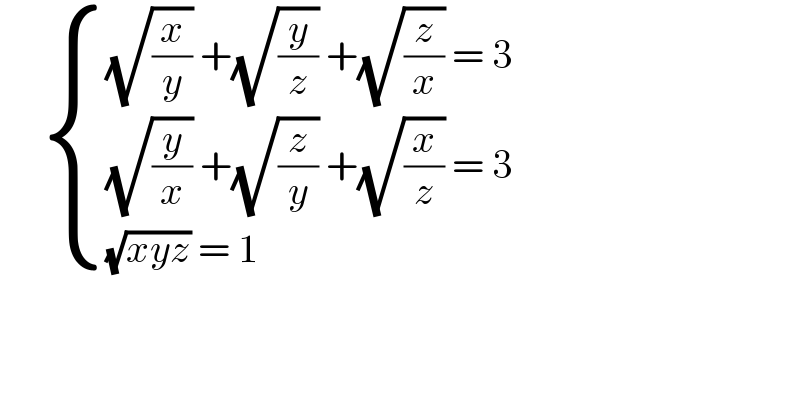
$$\:\:\:\:\:\begin{cases}{\sqrt{\frac{{x}}{{y}}}\:+\sqrt{\frac{{y}}{{z}}}\:+\sqrt{\frac{{z}}{{x}}}\:=\:\mathrm{3}}\\{\sqrt{\frac{{y}}{{x}}}\:+\sqrt{\frac{{z}}{{y}}}\:+\sqrt{\frac{{x}}{{z}}}\:=\:\mathrm{3}}\\{\sqrt{{xyz}}\:=\:\mathrm{1}}\end{cases} \\ $$$$\: \\ $$$$ \\ $$
Answered by mr W last updated on 27/Dec/22
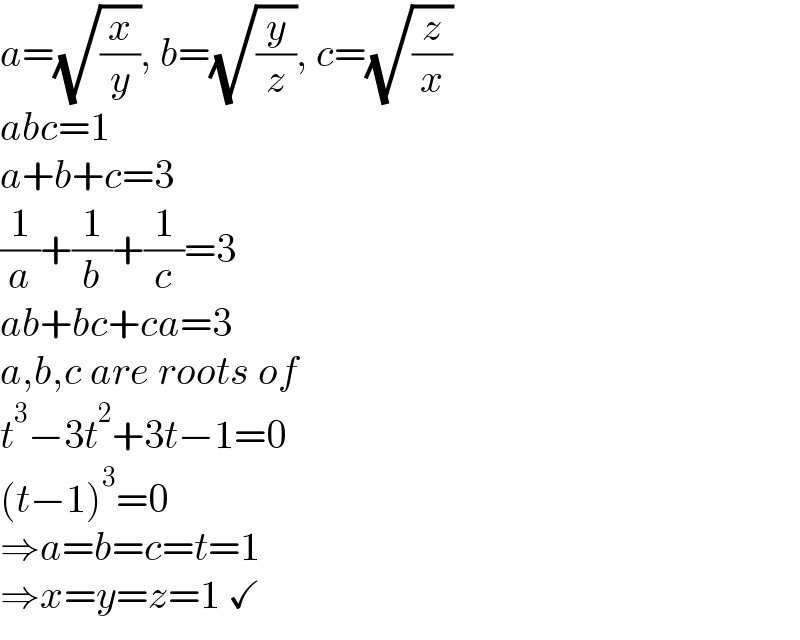
$${a}=\sqrt{\frac{{x}}{{y}}},\:{b}=\sqrt{\frac{{y}}{{z}}},\:{c}=\sqrt{\frac{{z}}{{x}}} \\ $$$${abc}=\mathrm{1} \\ $$$${a}+{b}+{c}=\mathrm{3} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\mathrm{3} \\ $$$${ab}+{bc}+{ca}=\mathrm{3} \\ $$$${a},{b},{c}\:{are}\:{roots}\:{of} \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow{a}={b}={c}={t}=\mathrm{1} \\ $$$$\Rightarrow{x}={y}={z}=\mathrm{1}\:\checkmark \\ $$
