
Question Number 183583 by Acem last updated on 27/Dec/22

Commented by Acem last updated on 27/Dec/22

$${A}\:{stone}\:{of}\:\mathrm{40}\:{kg},\:{i}'{ve}\:{cut}\:{it}\:{into}\:\mathrm{4}\:{diferent}\:{parts}, \\ $$$$\:{now}\:{i}\:{can}\:{use}\:{them}\:{for}\:{measure}\:{weights}\:\mathrm{1}−\mathrm{40}\:{Kg}\: \\ $$$$\:{Sure}\:{the}\:{qusetion}\:{is}\:{weight}\:{of}\:{each}\:{piece}? \\ $$$$\:{But}\:{by}\:{a}\:{logical}\:{solution}\:{not}\:{by}\:{experiment},\:{please}! \\ $$$$ \\ $$
Answered by CrispyXYZ last updated on 27/Dec/22

$$\mathrm{1},\:\mathrm{3},\:\mathrm{9},\:\mathrm{27}? \\ $$
Commented by Matica last updated on 27/Dec/22
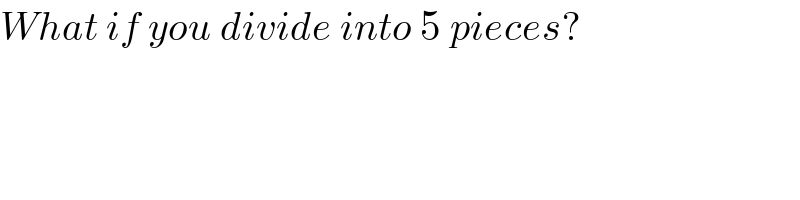
$${What}\:{if}\:{you}\:{divide}\:{into}\:\mathrm{5}\:{pieces}? \\ $$
Commented by CrispyXYZ last updated on 27/Dec/22

$$\mathrm{Each}\:\mathrm{piece}\:\mathrm{of}\:\mathrm{stone}\:\mathrm{can}\:\mathrm{be}\:\mathrm{placed}\:\mathrm{on}\: \\ $$$$\mathrm{the}\:\mathrm{right}\left(+\right),\:\mathrm{left}\left(−\right),\:\mathrm{or}\:\mathrm{not}\left(\mathrm{0}\right). \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{consider}\:\mathrm{trinary}\left(\mathrm{base}\:\mathrm{3}\right) \\ $$$$\mathrm{there}\:\mathrm{are}\:\mathrm{4}\:\mathrm{digits}\:\mathrm{in}\:\mathrm{total} \\ $$$$\mathrm{3}^{\mathrm{0}} +\mathrm{3}^{\mathrm{1}} +\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} =\mathrm{40} \\ $$$$\mathrm{each}\:\mathrm{piece}=\mathrm{3}^{\mathrm{0}} ,\:\mathrm{3}^{\mathrm{1}} ,\mathrm{3}^{\mathrm{2}} ,\mathrm{3}^{\mathrm{3}} \\ $$
Commented by Rasheed.Sindhi last updated on 27/Dec/22

$${With}\:\mathrm{5}\:{such}\:'{measures}'\:\left(\mathrm{1},\mathrm{3},\mathrm{9},\mathrm{27},\mathrm{81}\right) \\ $$$${you}\:{can}\:{weigh}\:{upto}\:\mathrm{121}\:{kg}. \\ $$
Commented by Rasheed.Sindhi last updated on 27/Dec/22

$${you}\:{can}\:{break}\:{ino}\:\mathrm{2}\:{pieces}\:{of}\:{any}\:{one} \\ $$$$\left({except}\:\mathrm{1}\:{of}\:{course}\right)\:{to}\:{make}\:{it} \\ $$$$'\mathrm{5}\:{peices}'.\:{For}\:{example}\:: \\ $$$$\mathrm{1},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{27}\:{but}\:{this}\:{will}\:{make}\:{your} \\ $$$${question}\:{somewhat}\:{inefficient}. \\ $$$${Because}\:{four}\:{peices}\:{are} \\ $$$$\:{minimumly}\:{required}\:{and}\:{with}\:{it} \\ $$$${the}\:{question}\:{has}\:{unique}\:{solution}. \\ $$$$\left({You}\:{can}'{t}\:{do}\:{this}\:{by}\:\mathrm{3}\:{peices}\:{of}\:\mathrm{40}\:{kg}\right) \\ $$
