
Question Number 183559 by cortano1 last updated on 27/Dec/22
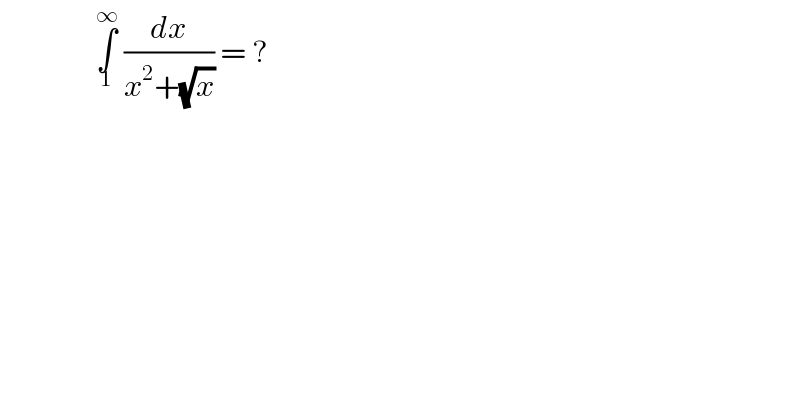
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{\mathrm{1}} {\overset{\infty} {\int}}\:\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{{x}}}\:=\:?\: \\ $$
Answered by greougoury555 last updated on 27/Dec/22
![G = ∫_1 ^( ∞) (dx/(x^2 +(√x))) = ∫_1 ^( ∞) ((2du)/(u^3 +1)) = (1/3) [ ∫_1 ^( ∞) ( (2/(u+1))−((2u−4)/(u^2 −u+1))) du ] = (1/3) [ 2ln ∣u+1∣−∫_1 ^( ∞) ((2(u−(1/2))−3)/((u−(1/2))^2 +(3/4))) du ] = (1/3) [ 2ln ∣u+1∣ −ln ((u−(1/2))^2 +(3/4))+2(√3) tan^(−1) (((2(u−(1/2)))/( (√3)))) ]_1 ^∞ = (1/3) [ ln ∣(((u+1)^2 )/(u^2 −u+1))∣+2(√3) tan^(−1) (((2u−1)/( (√3))))]_1 ^∞ = ((2π)/(3(√3)))−ln (4)^(1/3) = ((2π(√3))/9) −ln (4)^(1/3)](Q183597.png)
$$\:\:\:{G}\:=\:\int_{\mathrm{1}} ^{\:\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{{x}}}\:=\:\int_{\mathrm{1}} ^{\:\infty} \:\frac{\mathrm{2}{du}}{{u}^{\mathrm{3}} +\mathrm{1}}\: \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left[\:\int_{\mathrm{1}} ^{\:\infty} \left(\:\frac{\mathrm{2}}{{u}+\mathrm{1}}−\frac{\mathrm{2}{u}−\mathrm{4}}{{u}^{\mathrm{2}} −{u}+\mathrm{1}}\right)\:{du}\:\right] \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left[\:\mathrm{2ln}\:\mid{u}+\mathrm{1}\mid−\int_{\mathrm{1}} ^{\:\infty} \frac{\mathrm{2}\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{3}}{\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\:{du}\:\right] \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left[\:\mathrm{2ln}\:\mid{u}+\mathrm{1}\mid\:−\mathrm{ln}\:\left(\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right)+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{3}}}\right)\:\right]_{\mathrm{1}} ^{\infty} \: \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left[\:\mathrm{ln}\:\mid\frac{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{2}} −{u}+\mathrm{1}}\mid+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{u}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}−\mathrm{ln}\:\sqrt[{\mathrm{3}}]{\mathrm{4}}\: \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}\:−\mathrm{ln}\:\sqrt[{\mathrm{3}}]{\mathrm{4}}\: \\ $$
