
Question Number 183536 by SANOGO last updated on 26/Dec/22
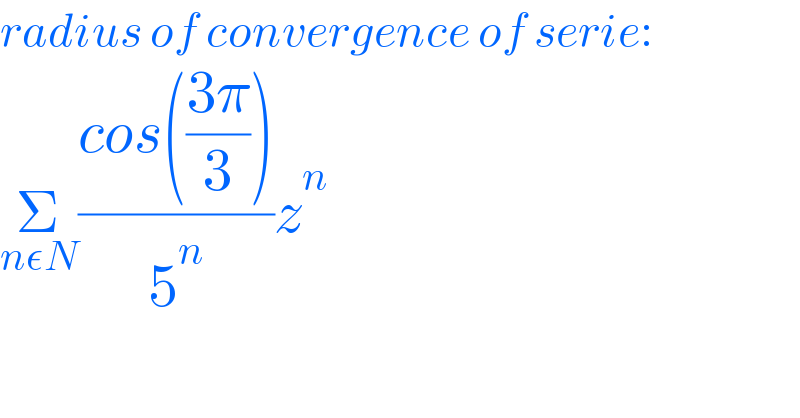
$${radius}\:{of}\:{convergence}\:{of}\:{serie}: \\ $$$$\underset{{n}\epsilon{N}} {\sum}\frac{{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{3}}\right)}{\mathrm{5}^{{n}} }{z}^{{n}} \\ $$
Commented by mr W last updated on 26/Dec/22
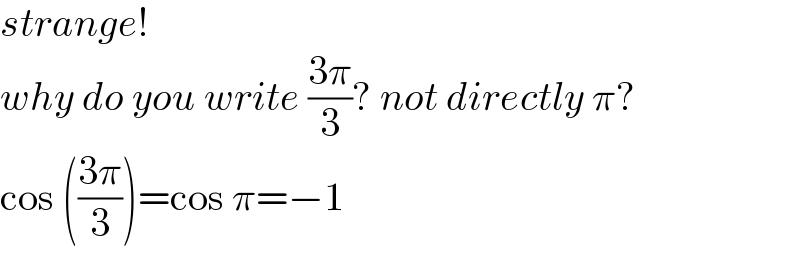
$${strange}! \\ $$$${why}\:{do}\:{you}\:{write}\:\frac{\mathrm{3}\pi}{\mathrm{3}}?\:{not}\:{directly}\:\pi? \\ $$$$\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{3}}\right)=\mathrm{cos}\:\pi=−\mathrm{1} \\ $$
Answered by aleks041103 last updated on 27/Dec/22
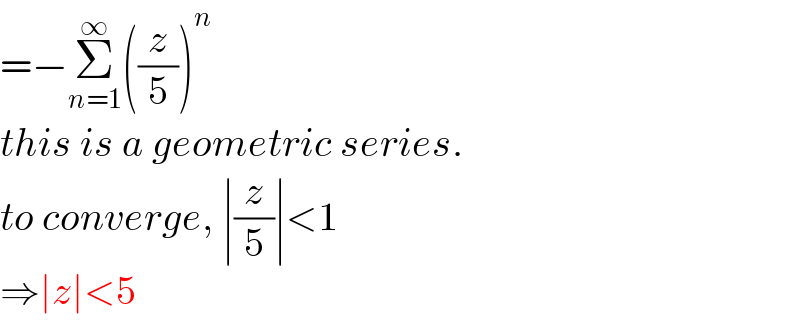
$$=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{{z}}{\mathrm{5}}\right)^{{n}} \\ $$$${this}\:{is}\:{a}\:{geometric}\:{series}. \\ $$$${to}\:{converge},\:\mid\frac{{z}}{\mathrm{5}}\mid<\mathrm{1} \\ $$$$\Rightarrow\mid{z}\mid<\mathrm{5} \\ $$
