
Question Number 183527 by aurpeyz last updated on 26/Dec/22

Commented by aurpeyz last updated on 26/Dec/22

$${The}\:{bar}\:{is}\:{under}\:{the}\:{action}\:{of}\:{axial}\: \\ $$$${concentrated}\:{force}\:{P}\:{and}\:\mathrm{2}{P}\:\left({P}=\mathrm{10}{KN}\right). \\ $$$${Area}\:{of}\:{constant}\:{cross}\:{section}\:{of}\:{bar}\:{is} \\ $$$${equal}\:{F},\:{Young}'{s}\:{modulus}\:{of}\:{bar}\:{material} \\ $$$${is}\:{equal}\:{E}.\: \\ $$$${Determine}\:{the}\:{maximum}\:{value}\:{of}\:{the}\: \\ $$$${longitudinal}\:{force}\:{N}_{{x}} \:{in}\:{the}\:{power}\:{sections}. \\ $$$${a}.\:\mathrm{12}.\mathrm{5}{KN} \\ $$$${b}.\:\mathrm{10}{KN} \\ $$$${c}.\:\mathrm{20}{KN} \\ $$$${d}.\:\mathrm{30}{KN} \\ $$
Commented by mr W last updated on 26/Dec/22
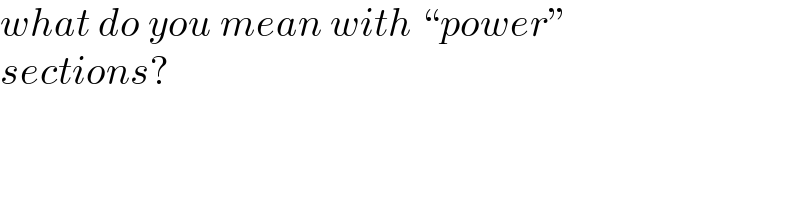
$${what}\:{do}\:{you}\:{mean}\:{with}\:``{power}''\: \\ $$$${sections}? \\ $$
Answered by mr W last updated on 26/Dec/22
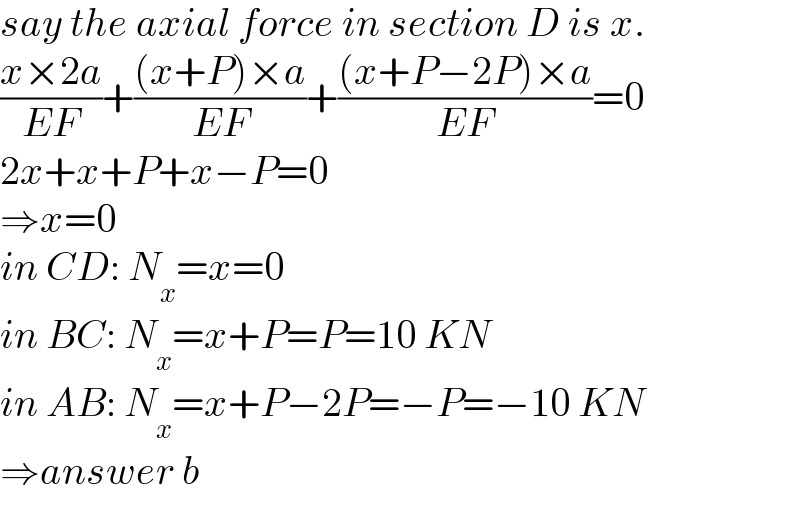
$${say}\:{the}\:{axial}\:{force}\:{in}\:{section}\:{D}\:{is}\:{x}. \\ $$$$\frac{{x}×\mathrm{2}{a}}{{EF}}+\frac{\left({x}+{P}\right)×{a}}{{EF}}+\frac{\left({x}+{P}−\mathrm{2}{P}\right)×{a}}{{EF}}=\mathrm{0} \\ $$$$\mathrm{2}{x}+{x}+{P}+{x}−{P}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{0} \\ $$$${in}\:{CD}:\:{N}_{{x}} ={x}=\mathrm{0} \\ $$$${in}\:{BC}:\:{N}_{{x}} ={x}+{P}={P}=\mathrm{10}\:{KN} \\ $$$${in}\:{AB}:\:{N}_{{x}} ={x}+{P}−\mathrm{2}{P}=−{P}=−\mathrm{10}\:{KN} \\ $$$$\Rightarrow{answer}\:{b} \\ $$
Commented by aurpeyz last updated on 27/Dec/22

$${thanks} \\ $$
