
Question Number 183440 by aurpeyz last updated on 25/Dec/22
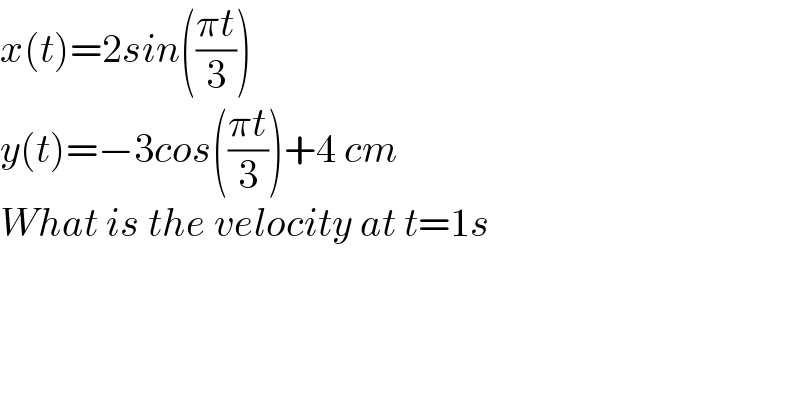
$${x}\left({t}\right)=\mathrm{2}{sin}\left(\frac{\pi{t}}{\mathrm{3}}\right) \\ $$$${y}\left({t}\right)=−\mathrm{3}{cos}\left(\frac{\pi{t}}{\mathrm{3}}\right)+\mathrm{4}\:{cm} \\ $$$${What}\:{is}\:{the}\:{velocity}\:{at}\:{t}=\mathrm{1}{s} \\ $$
Answered by cortano1 last updated on 26/Dec/22
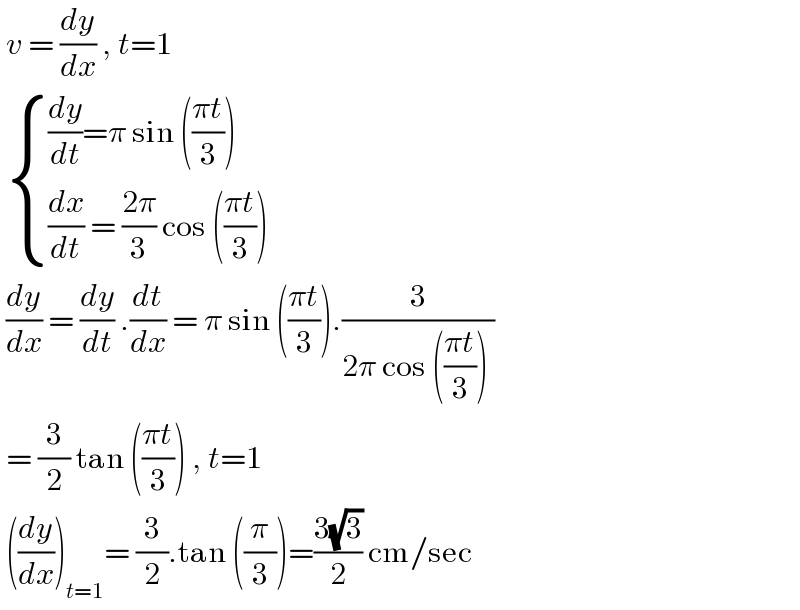
$$\:{v}\:=\:\frac{{dy}}{{dx}}\:,\:{t}=\mathrm{1}\: \\ $$$$\:\begin{cases}{\frac{{dy}}{{dt}}=\pi\:\mathrm{sin}\:\left(\frac{\pi{t}}{\mathrm{3}}\right)}\\{\frac{{dx}}{{dt}}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:\mathrm{cos}\:\left(\frac{\pi{t}}{\mathrm{3}}\right)}\end{cases} \\ $$$$\:\frac{{dy}}{{dx}}\:=\:\frac{{dy}}{{dt}}\:.\frac{{dt}}{{dx}}\:=\:\pi\:\mathrm{sin}\:\left(\frac{\pi{t}}{\mathrm{3}}\right).\frac{\mathrm{3}}{\mathrm{2}\pi\:\mathrm{cos}\:\left(\frac{\pi{t}}{\mathrm{3}}\right)\:} \\ $$$$\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{tan}\:\left(\frac{\pi{t}}{\mathrm{3}}\right)\:,\:{t}=\mathrm{1} \\ $$$$\:\left(\frac{{dy}}{{dx}}\right)_{{t}=\mathrm{1}} =\:\frac{\mathrm{3}}{\mathrm{2}}.\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}\right)=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cm}/\mathrm{sec} \\ $$
Commented by mr W last updated on 26/Dec/22
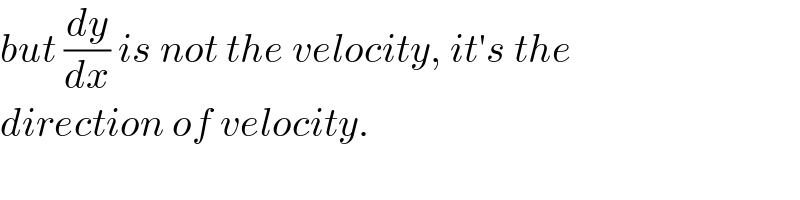
$${but}\:\frac{{dy}}{{dx}}\:{is}\:{not}\:{the}\:{velocity},\:{it}'{s}\:{the}\: \\ $$$${direction}\:{of}\:{velocity}. \\ $$
Answered by mr W last updated on 26/Dec/22
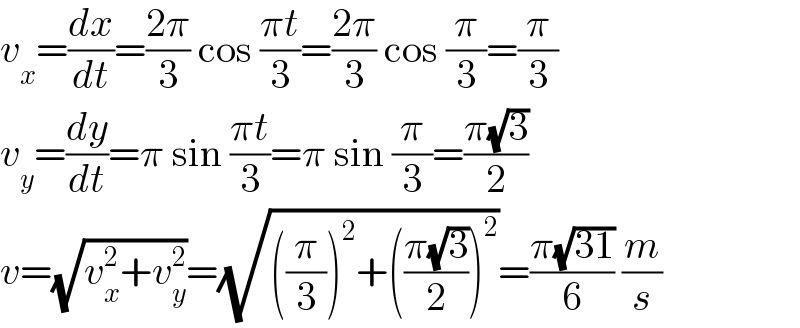
$${v}_{{x}} =\frac{{dx}}{{dt}}=\frac{\mathrm{2}\pi}{\mathrm{3}}\:\mathrm{cos}\:\frac{\pi{t}}{\mathrm{3}}=\frac{\mathrm{2}\pi}{\mathrm{3}}\:\mathrm{cos}\:\frac{\pi}{\mathrm{3}}=\frac{\pi}{\mathrm{3}} \\ $$$${v}_{{y}} =\frac{{dy}}{{dt}}=\pi\:\mathrm{sin}\:\frac{\pi{t}}{\mathrm{3}}=\pi\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${v}=\sqrt{{v}_{{x}} ^{\mathrm{2}} +{v}_{{y}} ^{\mathrm{2}} }=\sqrt{\left(\frac{\pi}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\pi\sqrt{\mathrm{31}}}{\mathrm{6}}\:\frac{{m}}{{s}} \\ $$
Commented by aurpeyz last updated on 26/Dec/22
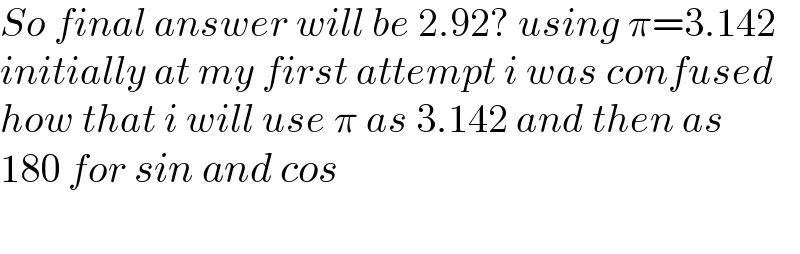
$${So}\:{final}\:{answer}\:{will}\:{be}\:\mathrm{2}.\mathrm{92}?\:{using}\:\pi=\mathrm{3}.\mathrm{142} \\ $$$${initially}\:{at}\:{my}\:{first}\:{attempt}\:{i}\:{was}\:{confused} \\ $$$${how}\:{that}\:{i}\:{will}\:{use}\:\pi\:{as}\:\mathrm{3}.\mathrm{142}\:{and}\:{then}\:{as} \\ $$$$\mathrm{180}\:{for}\:{sin}\:{and}\:{cos} \\ $$$$ \\ $$
