
Question Number 183426 by a.lgnaoui last updated on 25/Dec/22

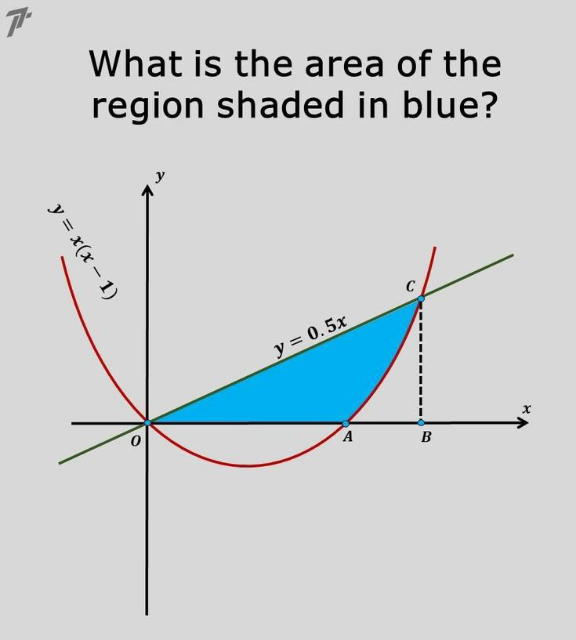
$${surface}\:{de}\:{la}\:{partie}\:{bleu} \\ $$$${du}\:{graphe}? \\ $$
Commented by a.lgnaoui last updated on 25/Dec/22
Commented by cherokeesay last updated on 25/Dec/22
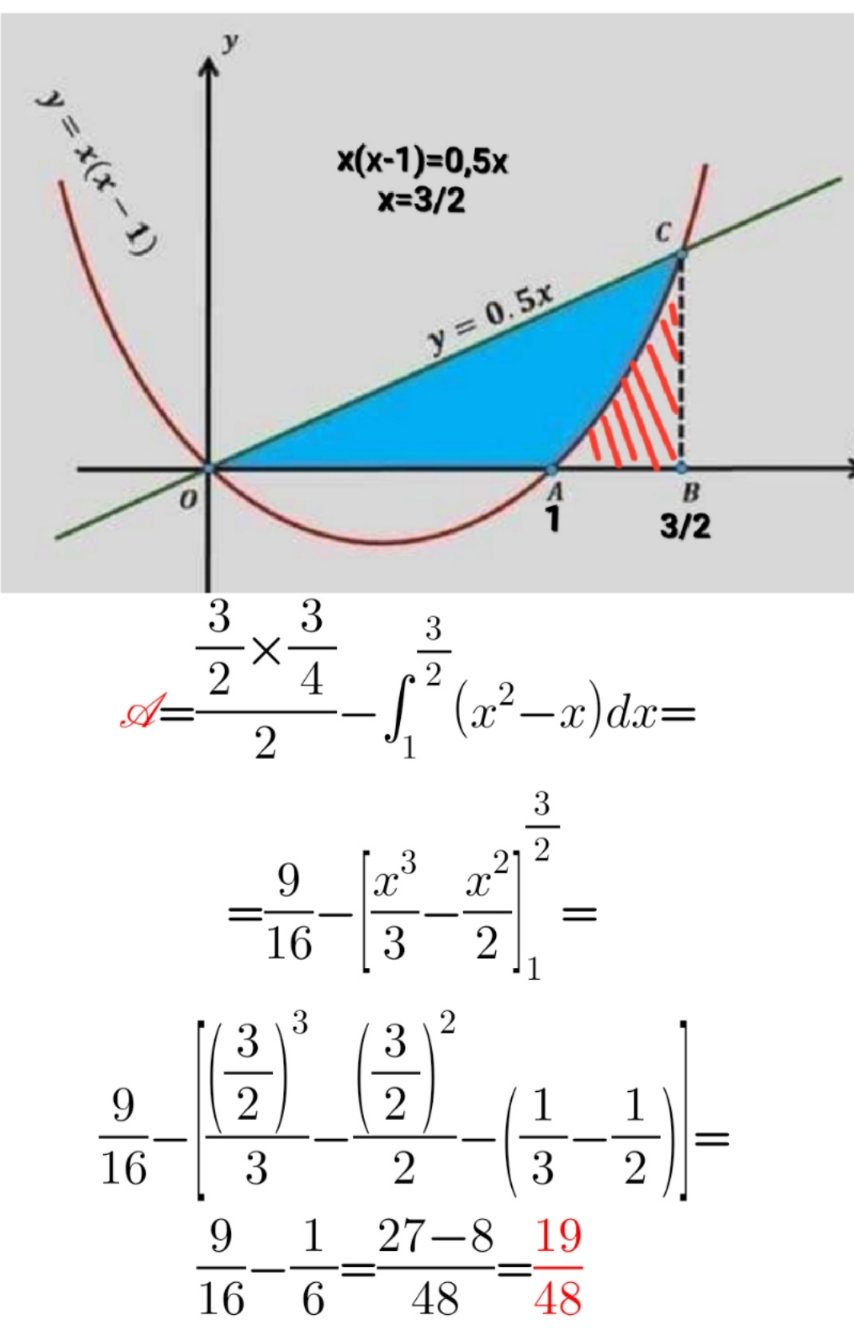
Commented by a.lgnaoui last updated on 26/Dec/22

$${thank}\:{you} \\ $$
Answered by Acem last updated on 26/Dec/22
![Surf.= (1/4) + ∫_1 ^( (3/2)) ((3/2) x −x^2 )dx = (1/4) +[ x^2 ((3/4) −(1/3) x)]_1 ^(3/2) = (1/4) + (9/(16)) − (5/(12)) = (1/4) +(7/(48)) = ((19)/(48 )) un^2](Q183449.png)
$$ \\ $$$$\:{Surf}.=\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\int_{\mathrm{1}} ^{\:\:\frac{\mathrm{3}}{\mathrm{2}}} \left(\frac{\mathrm{3}}{\mathrm{2}}\:{x}\:−{x}^{\mathrm{2}} \right){dx} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:+\left[\:{x}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{3}}\:{x}\right)\right]_{\mathrm{1}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{9}}{\mathrm{16}}\:−\:\frac{\mathrm{5}}{\mathrm{12}}\:=\:\:\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{7}}{\mathrm{48}}\:\:=\:\:\:\frac{\mathrm{19}}{\mathrm{48}\:}\:{un}^{\mathrm{2}} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 26/Dec/22

$${thank}\:{you}\: \\ $$
Answered by mr W last updated on 26/Dec/22
![a way without integral: x(x−1)−0.5x=0 ⇒x^2 −1.5x=0 ⇒A_1 =(([(−1.5)^2 −4×1×0]^(3/2) )/(6×1^2 ))=((27)/(48)) x(x−1)−0=0 ⇒x^2 −x=0 ⇒A_2 =(([(−1)^2 −4×1×0]^(3/2) )/(6×1^2 ))=(1/6) A_(blue) =A_1 −A_2 =((27)/(48))−(1/6)=((19)/(48)) ✓](Q183462.png)
$$\boldsymbol{{a}}\:\boldsymbol{{way}}\:\boldsymbol{{without}}\:\boldsymbol{{integral}}: \\ $$$${x}\left({x}−\mathrm{1}\right)−\mathrm{0}.\mathrm{5}{x}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} −\mathrm{1}.\mathrm{5}{x}=\mathrm{0} \\ $$$$\Rightarrow{A}_{\mathrm{1}} =\frac{\left[\left(−\mathrm{1}.\mathrm{5}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{1}×\mathrm{0}\right]^{\mathrm{3}/\mathrm{2}} }{\mathrm{6}×\mathrm{1}^{\mathrm{2}} }=\frac{\mathrm{27}}{\mathrm{48}} \\ $$$${x}\left({x}−\mathrm{1}\right)−\mathrm{0}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} −{x}=\mathrm{0} \\ $$$$\Rightarrow{A}_{\mathrm{2}} =\frac{\left[\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{1}×\mathrm{0}\right]^{\mathrm{3}/\mathrm{2}} }{\mathrm{6}×\mathrm{1}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${A}_{{blue}} ={A}_{\mathrm{1}} −{A}_{\mathrm{2}} =\frac{\mathrm{27}}{\mathrm{48}}−\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{19}}{\mathrm{48}}\:\:\checkmark \\ $$
Commented by Matica last updated on 27/Dec/22
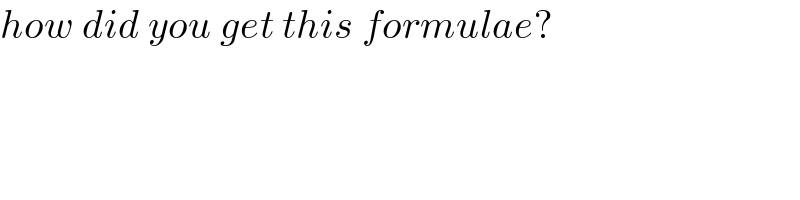
$${how}\:{did}\:{you}\:{get}\:{this}\:{formulae}? \\ $$
Commented by mr W last updated on 27/Dec/22

$${A}=\frac{\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{6}{a}^{\mathrm{2}} } \\ $$$${for}\:{more}\:{see}\:{Q}\mathrm{89781} \\ $$
Commented by Matica last updated on 27/Dec/22

$${Thank}\:{you}! \\ $$
