
Question Number 183420 by mokys last updated on 25/Dec/22
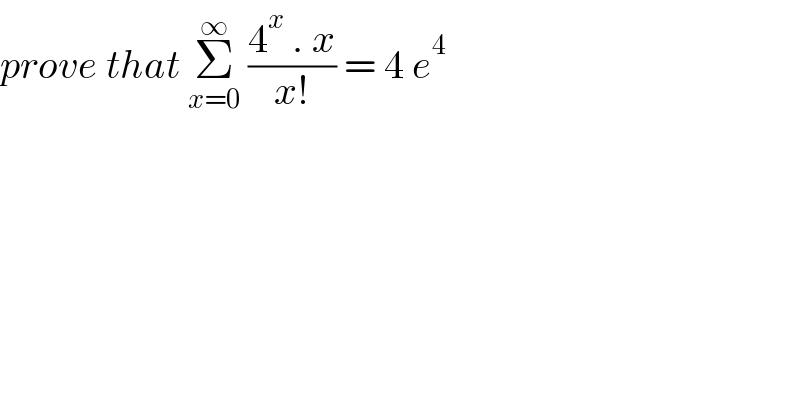
$${prove}\:{that}\:\underset{{x}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{4}^{{x}} \:.\:{x}}{{x}!}\:=\:\mathrm{4}\:{e}^{\mathrm{4}} \\ $$
Answered by Ar Brandon last updated on 25/Dec/22
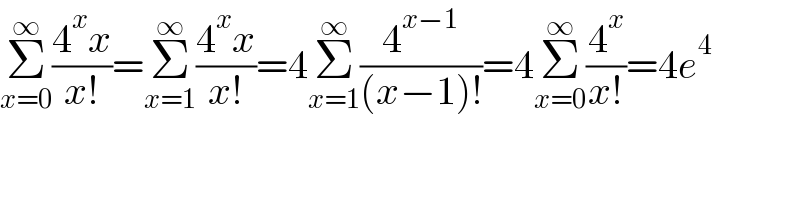
$$\underset{{x}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{{x}} {x}}{{x}!}=\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{{x}} {x}}{{x}!}=\mathrm{4}\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{{x}−\mathrm{1}} }{\left({x}−\mathrm{1}\right)!}=\mathrm{4}\underset{{x}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{{x}} }{{x}!}=\mathrm{4}{e}^{\mathrm{4}} \\ $$
Answered by mr W last updated on 26/Dec/22
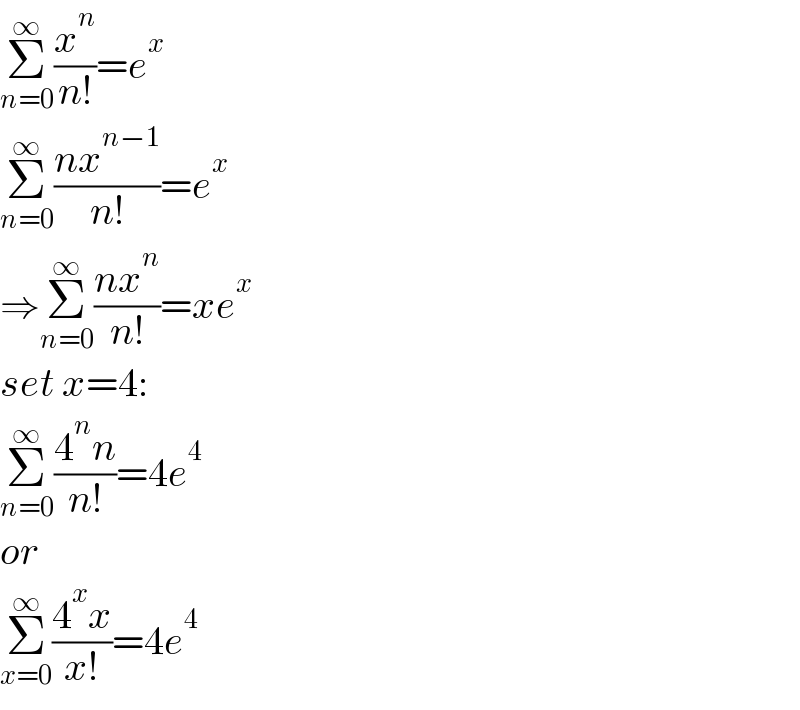
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!}={e}^{{x}} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{nx}^{{n}−\mathrm{1}} }{{n}!}={e}^{{x}} \\ $$$$\Rightarrow\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{nx}^{{n}} }{{n}!}={xe}^{{x}} \\ $$$${set}\:{x}=\mathrm{4}: \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{{n}} {n}}{{n}!}=\mathrm{4}{e}^{\mathrm{4}} \\ $$$${or} \\ $$$$\underset{{x}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{{x}} {x}}{{x}!}=\mathrm{4}{e}^{\mathrm{4}} \\ $$
