
Question Number 183380 by Shrinava last updated on 25/Dec/22
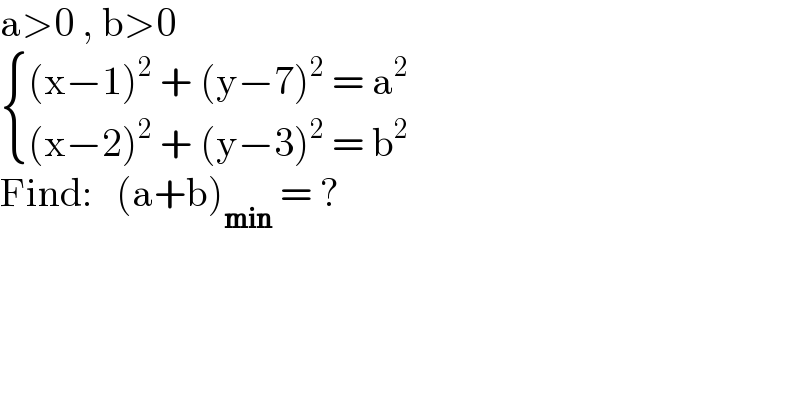
$$\mathrm{a}>\mathrm{0}\:,\:\mathrm{b}>\mathrm{0} \\ $$ $$\begin{cases}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:+\:\left(\mathrm{y}−\mathrm{7}\right)^{\mathrm{2}} \:=\:\mathrm{a}^{\mathrm{2}} }\\{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \:+\:\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} \:=\:\mathrm{b}^{\mathrm{2}} }\end{cases} \\ $$ $$\mathrm{Find}:\:\:\:\left(\mathrm{a}+\mathrm{b}\right)_{\boldsymbol{\mathrm{min}}} \:=\:? \\ $$
Commented byFrix last updated on 25/Dec/22

$$\sqrt{\mathrm{17}}=\:\mathrm{the}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{the}\:\mathrm{centers} \\ $$ $$\mathrm{If}\:\mathrm{we}\:\mathrm{see}\:\mathrm{it}\:\mathrm{as}\:\mathrm{two}\:\mathrm{independent}\:\mathrm{circles} \\ $$ $$\mathrm{obviously}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{0} \\ $$
