
Question Number 183227 by mr W last updated on 23/Dec/22
Commented by mr W last updated on 23/Dec/22
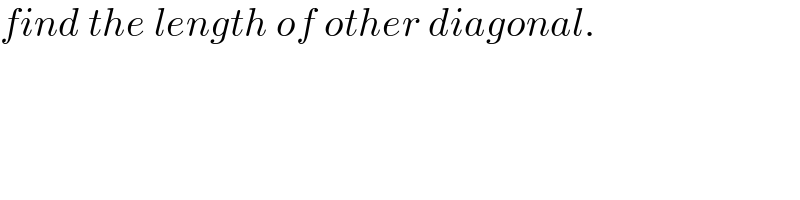
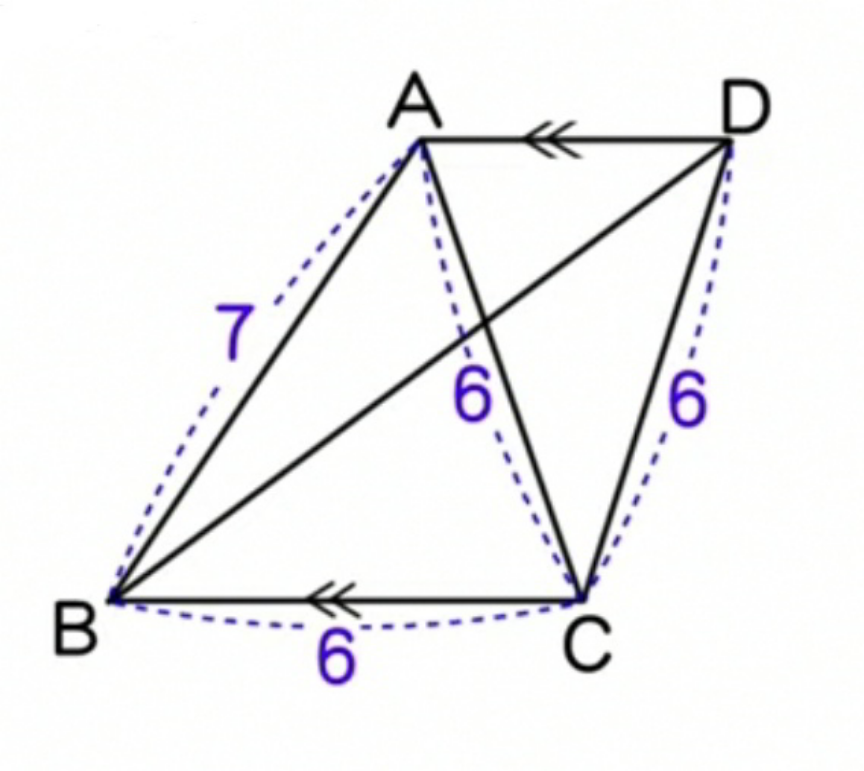
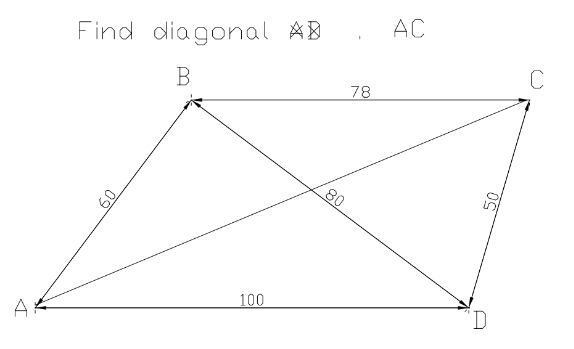
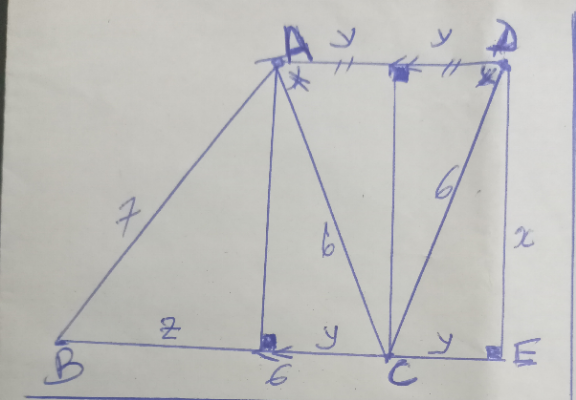
$${find}\:{the}\:{length}\:{of}\:{other}\:{diagonal}. \\ $$
Answered by mr W last updated on 24/Dec/22
Commented by mr W last updated on 24/Dec/22
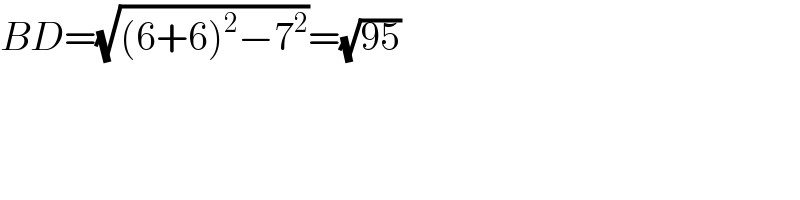
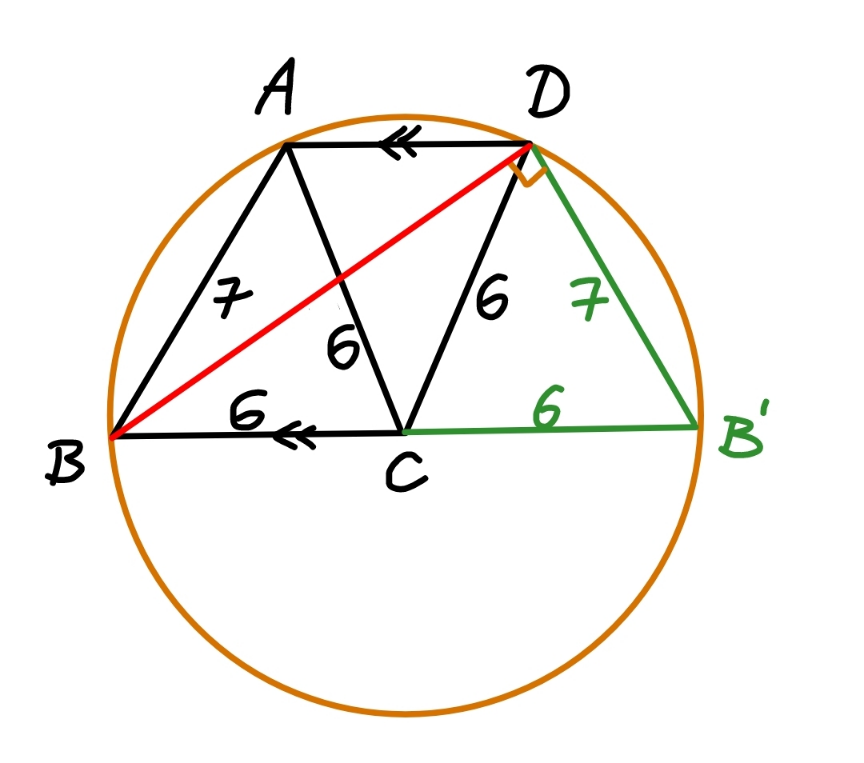
$${BD}=\sqrt{\left(\mathrm{6}+\mathrm{6}\right)^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }=\sqrt{\mathrm{95}} \\ $$
Commented by manxsol last updated on 24/Dec/22

$${We}\:{did}\:{not}\:{have}\:{the} \\ $$$$\:{vision}\:{but}\:{it}\:{is}\:{a}\: \\ $$$${special}\:{case}.\:{I}\:{send}\:{another} \\ $$$$\:{case} \\ $$
Commented by manxsol last updated on 24/Dec/22
Commented by mr W last updated on 24/Dec/22

$${yes}\:{it}'{s}\:{a}\:{special}\:{case}.\:{but}\:{the}\:{question} \\ $$$${only}\:{requests}\:{you}\:{to}\:{solve}\:{this}\:{special} \\ $$$${case},\:{nothing}\:{else}. \\ $$
Commented by mr W last updated on 24/Dec/22

$${as}\:{for}\:{the}\:{case}\:{you}\:{sent},\:{see}\:{Q}\mathrm{183281} \\ $$
Commented by manxsol last updated on 24/Dec/22
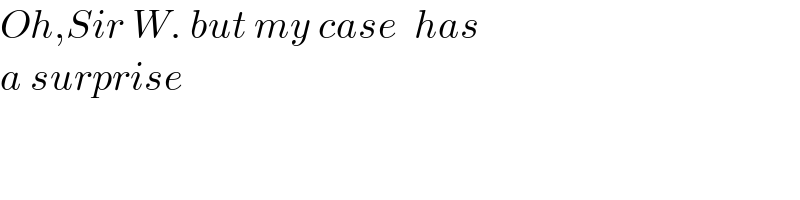
$${Oh},{Sir}\:{W}.\:{but}\:{my}\:{case}\:\:{has} \\ $$$${a}\:{surprise} \\ $$
Answered by Frix last updated on 23/Dec/22
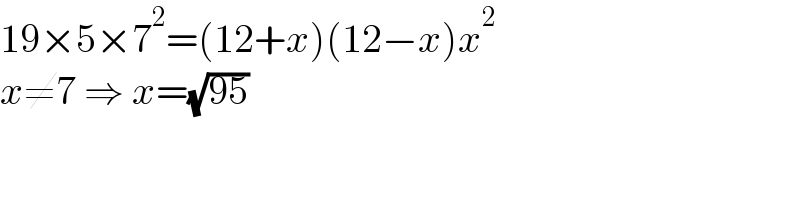
$$\mathrm{19}×\mathrm{5}×\mathrm{7}^{\mathrm{2}} =\left(\mathrm{12}+{x}\right)\left(\mathrm{12}−{x}\right){x}^{\mathrm{2}} \\ $$$${x}\neq\mathrm{7}\:\Rightarrow\:{x}=\sqrt{\mathrm{95}} \\ $$
Answered by a.lgnaoui last updated on 23/Dec/22
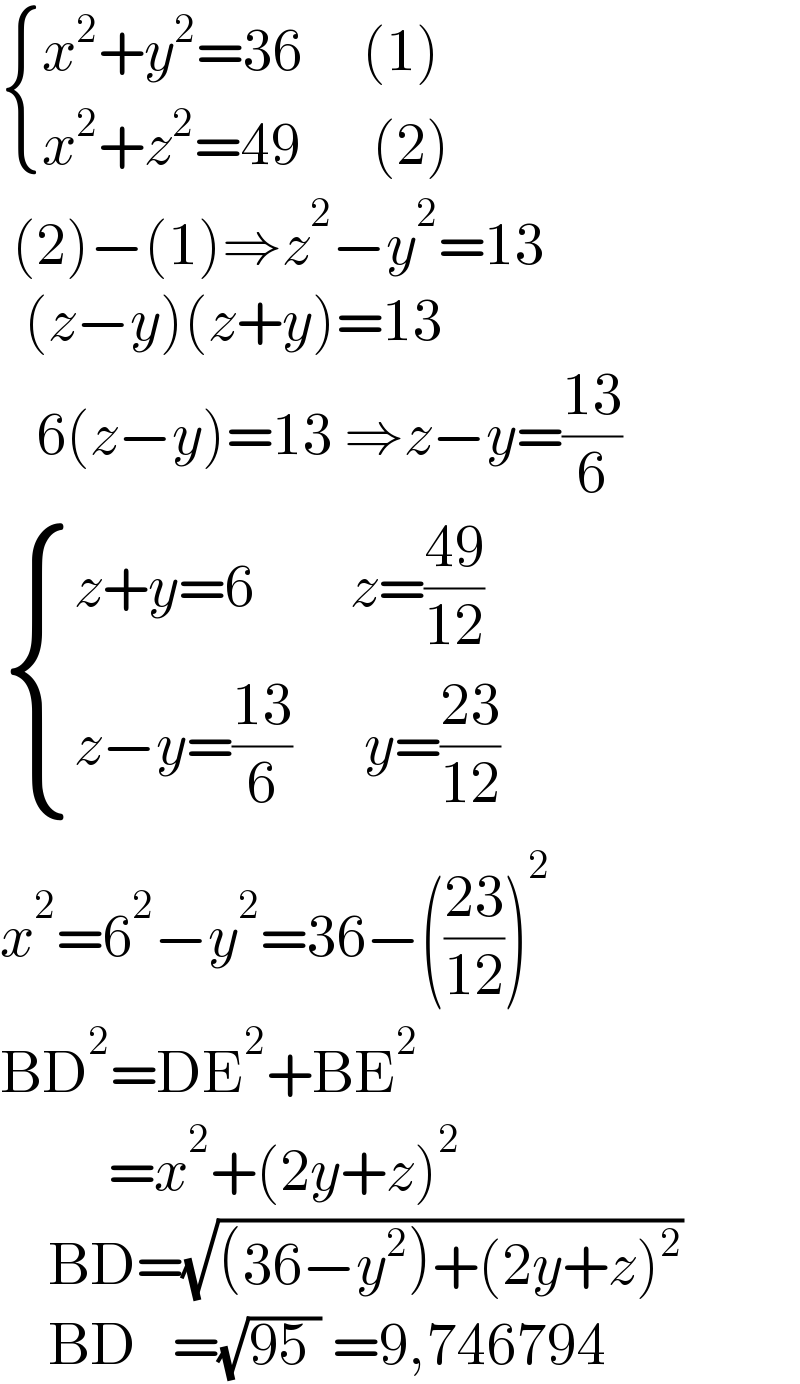
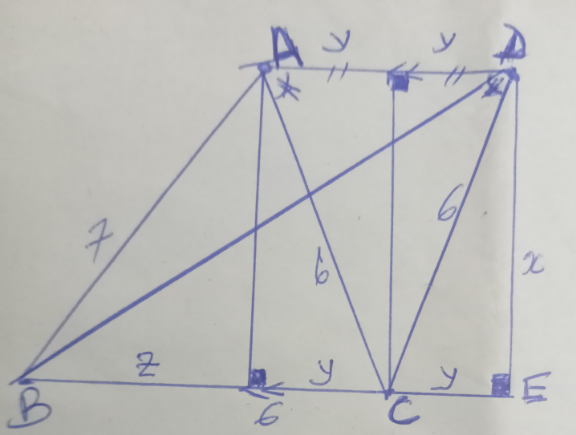
$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{36}\:\:\:\:\:\left(\mathrm{1}\right)}\\{{x}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{49}\:\:\:\:\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\:\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\Rightarrow{z}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{13} \\ $$$$\:\:\left({z}−{y}\right)\left({z}+{y}\right)=\mathrm{13} \\ $$$$\:\:\:\mathrm{6}\left({z}−{y}\right)=\mathrm{13}\:\Rightarrow{z}−{y}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\begin{cases}{{z}+{y}=\mathrm{6}\:\:\:\:\:\:\:\:{z}=\frac{\mathrm{49}}{\mathrm{12}}}\\{{z}−{y}=\frac{\mathrm{13}}{\mathrm{6}}\:\:\:\:\:\:{y}=\frac{\mathrm{23}}{\mathrm{12}}}\end{cases} \\ $$$${x}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{36}−\left(\frac{\mathrm{23}}{\mathrm{12}}\right)^{\mathrm{2}} \\ $$$$\mathrm{BD}^{\mathrm{2}} =\mathrm{DE}^{\mathrm{2}} +\mathrm{BE}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} +\left(\mathrm{2}{y}+{z}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{BD}=\sqrt{\left(\mathrm{36}−{y}^{\mathrm{2}} \right)+\left(\mathrm{2}{y}+{z}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\mathrm{BD}\:\:\:=\sqrt{\mathrm{95}\:}\:=\mathrm{9},\mathrm{746794} \\ $$
Commented by a.lgnaoui last updated on 23/Dec/22
Commented by a.lgnaoui last updated on 23/Dec/22
Answered by manxsol last updated on 23/Dec/22

