
Question Number 183205 by cortano1 last updated on 23/Dec/22

$$\:\:{Find}\:{the}\:{coefficient}\:{of}\:{x}^{\mathrm{11}} \:{in}\: \\ $$$$\:\left(\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{3}\right)^{\mathrm{6}} \:. \\ $$
Answered by mr W last updated on 23/Dec/22
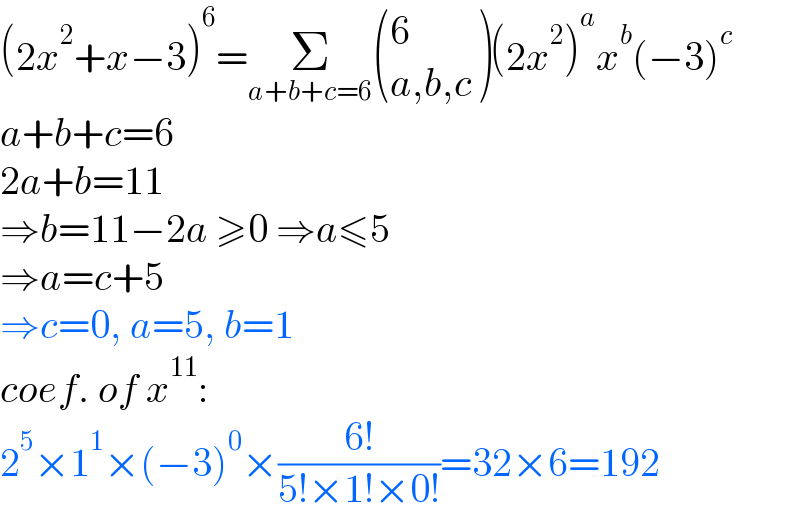
$$\left(\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{3}\right)^{\mathrm{6}} =\underset{{a}+{b}+{c}=\mathrm{6}} {\sum}\begin{pmatrix}{\mathrm{6}}\\{{a},{b},{c}}\end{pmatrix}\left(\mathrm{2}{x}^{\mathrm{2}} \right)^{{a}} {x}^{{b}} \left(−\mathrm{3}\right)^{{c}} \\ $$$${a}+{b}+{c}=\mathrm{6} \\ $$$$\mathrm{2}{a}+{b}=\mathrm{11} \\ $$$$\Rightarrow{b}=\mathrm{11}−\mathrm{2}{a}\:\geqslant\mathrm{0}\:\Rightarrow{a}\leqslant\mathrm{5} \\ $$$$\Rightarrow{a}={c}+\mathrm{5} \\ $$$$\Rightarrow{c}=\mathrm{0},\:{a}=\mathrm{5},\:{b}=\mathrm{1} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{11}} : \\ $$$$\mathrm{2}^{\mathrm{5}} ×\mathrm{1}^{\mathrm{1}} ×\left(−\mathrm{3}\right)^{\mathrm{0}} ×\frac{\mathrm{6}!}{\mathrm{5}!×\mathrm{1}!×\mathrm{0}!}=\mathrm{32}×\mathrm{6}=\mathrm{192} \\ $$
Answered by cortano1 last updated on 24/Dec/22
![⇒(2x^2 +x−3)^6 = 64x^(12) (1+(1/2)x^(−1) −(3/2)x^(−2) )^6 = 64x^(12) .Σ_(0≤a,b,c≤6) ^(a+b+c=6) ((( 6)),((a,b,c)) ) (1^a )((1/2)x^(−1) )^b (−(3/2)x^(−2) )^c [ −b−2c = −1, b+2c=1 ∧ a+b+c = 6] ∵ c = 0 , b=1 , a=5 Coefficient of x^(11) is 64×((6!)/(5!.1!.0!)) ×(1/2) = 64×3 = 192](Q183242.png)
$$\:\Rightarrow\left(\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{3}\right)^{\mathrm{6}} =\:\mathrm{64}{x}^{\mathrm{12}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{−\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{2}}{x}^{−\mathrm{2}} \right)^{\mathrm{6}} \\ $$$$\:=\:\mathrm{64}{x}^{\mathrm{12}} \:.\underset{\mathrm{0}\leqslant{a},{b},{c}\leqslant\mathrm{6}} {\overset{{a}+{b}+{c}=\mathrm{6}} {\sum}}\:\begin{pmatrix}{\:\:\:\:\mathrm{6}}\\{{a},{b},{c}}\end{pmatrix}\:\left(\mathrm{1}^{{a}} \right)\left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{−\mathrm{1}} \right)^{{b}} \left(−\frac{\mathrm{3}}{\mathrm{2}}{x}^{−\mathrm{2}} \right)^{{c}} \\ $$$$\:\left[\:−{b}−\mathrm{2}{c}\:=\:−\mathrm{1},\:{b}+\mathrm{2}{c}=\mathrm{1}\:\wedge\:{a}+{b}+{c}\:=\:\mathrm{6}\right] \\ $$$$\:\because\:{c}\:=\:\mathrm{0}\:,\:{b}=\mathrm{1}\:,\:{a}=\mathrm{5}\: \\ $$$${Coefficient}\:{of}\:{x}^{\mathrm{11}} \:{is}\:\mathrm{64}×\frac{\mathrm{6}!}{\mathrm{5}!.\mathrm{1}!.\mathrm{0}!}\:×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\:\mathrm{64}×\mathrm{3}\:=\:\mathrm{192}\: \\ $$
