
Question Number 183120 by Shrinava last updated on 20/Dec/22

$$\mathrm{I}−\mathrm{Incenter}\:\mathrm{in}\:\:\bigtriangleup\mathrm{ABC} \\ $$$$\mathrm{A}\left(\mathrm{2},\mathrm{2}\right)\:,\:\mathrm{B}\left(\mathrm{6},\mathrm{4}\right)\:,\:\mathrm{C}\left(\mathrm{4},\mathrm{8}\right)\:,\:\mathrm{M}\left(\mathrm{8},\mathrm{6}\right) \\ $$$$\mathrm{Find}:\:\:\:\mathrm{MI}\:=\:? \\ $$
Answered by manolex last updated on 21/Dec/22
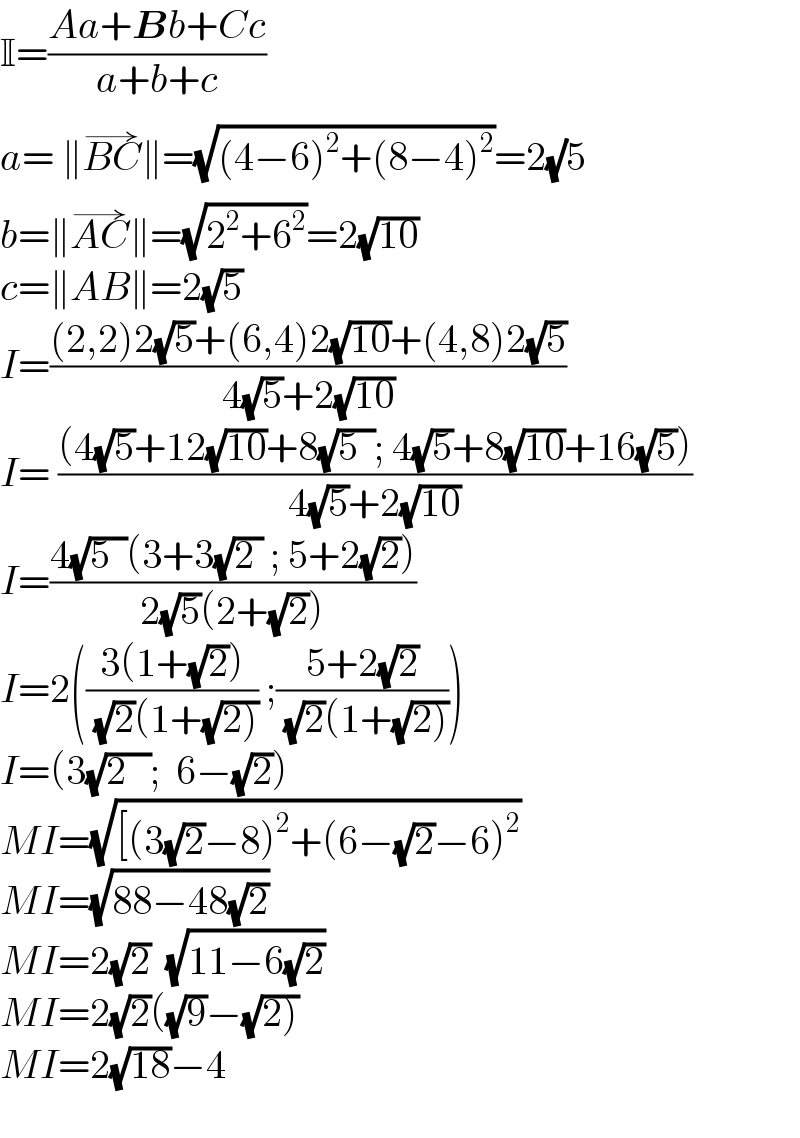
$$\mathbb{I}=\frac{{Aa}+\boldsymbol{{B}}{b}+{Cc}}{{a}+{b}+{c}} \\ $$$${a}=\:\parallel\overset{\rightarrow} {{BC}}\parallel=\sqrt{\left(\mathrm{4}−\mathrm{6}\right)^{\mathrm{2}} +\left(\mathrm{8}−\mathrm{4}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{}\mathrm{5} \\ $$$${b}=\parallel\overset{\rightarrow} {{AC}}\parallel=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{10}} \\ $$$${c}=\parallel{AB}\parallel=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$${I}=\frac{\left(\mathrm{2},\mathrm{2}\right)\mathrm{2}\sqrt{\mathrm{5}}+\left(\mathrm{6},\mathrm{4}\right)\mathrm{2}\sqrt{\mathrm{10}}+\left(\mathrm{4},\mathrm{8}\right)\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{10}}} \\ $$$${I}=\:\frac{\left(\mathrm{4}\sqrt{\mathrm{5}}+\mathrm{12}\sqrt{\mathrm{10}}+\mathrm{8}\sqrt{\mathrm{5}\:\:};\:\mathrm{4}\sqrt{\mathrm{5}}+\mathrm{8}\sqrt{\mathrm{10}}+\mathrm{16}\sqrt{\mathrm{5}}\right)}{\mathrm{4}\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{10}}} \\ $$$${I}=\frac{\mathrm{4}\sqrt{\mathrm{5}\:\:}\left(\mathrm{3}+\mathrm{3}\sqrt{\mathrm{2}\:}\:;\:\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{2}\sqrt{\mathrm{5}}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)} \\ $$$${I}=\mathrm{2}\left(\frac{\mathrm{3}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}\left(\mathrm{1}+\sqrt{\left.\mathrm{2}\right)}\right.}\:;\frac{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}\left(\mathrm{1}+\sqrt{\left.\mathrm{2}\right)}\right.}\right) \\ $$$${I}=\left(\mathrm{3}\sqrt{\mathrm{2}\:\:\:};\:\:\mathrm{6}−\sqrt{\mathrm{2}}\right) \\ $$$${MI}=\sqrt{\left[\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{8}\right)^{\mathrm{2}} +\left(\mathrm{6}−\sqrt{\mathrm{2}}−\mathrm{6}\right)^{\mathrm{2}} \right.} \\ $$$${MI}=\sqrt{\mathrm{88}−\mathrm{48}\sqrt{\mathrm{2}}} \\ $$$${MI}=\mathrm{2}\sqrt{\mathrm{2}}\:\:\sqrt{\mathrm{11}−\mathrm{6}\sqrt{\mathrm{2}}} \\ $$$${MI}=\mathrm{2}\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{9}}−\sqrt{\left.\mathrm{2}\right)}\right. \\ $$$${MI}=\mathrm{2}\sqrt{\mathrm{18}}−\mathrm{4} \\ $$$$ \\ $$
Answered by manolex last updated on 21/Dec/22
$$ \\ $$$$ \\ $$
