
Question Number 182984 by Mastermind last updated on 18/Dec/22

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{for}\:\mathrm{the}\:\mathrm{plane} \\ $$$$\mathrm{through}\:\mathrm{the}\:\mathrm{point}\:\mathrm{A}\left(\mathrm{6},\:\mathrm{2},\:−\mathrm{4}\right), \\ $$$$\mathrm{B}\left(−\mathrm{2},\:\mathrm{4},\:\mathrm{8}\right),\:\mathrm{C}\left(\mathrm{4},\:−\mathrm{2},\:\mathrm{2}\right).\:−\mathrm{Vector}\:\mathrm{Analysis} \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Answered by cortano1 last updated on 18/Dec/22
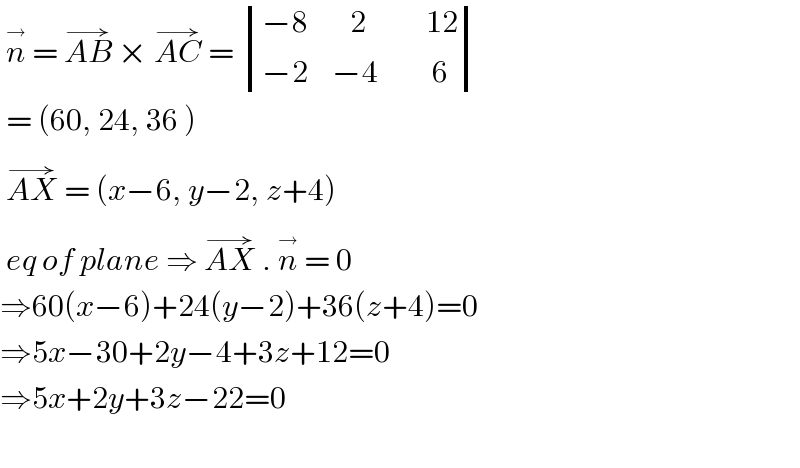
$$\:\overset{\rightarrow} {{n}}\:=\:\overset{\rightarrow} {{AB}}\:×\:\overset{\rightarrow} {{AC}}\:=\:\begin{vmatrix}{−\mathrm{8}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{12}}\\{−\mathrm{2}\:\:\:\:−\mathrm{4}\:\:\:\:\:\:\:\:\:\mathrm{6}}\end{vmatrix} \\ $$$$\:=\:\left(\mathrm{60},\:\mathrm{24},\:\mathrm{36}\:\right) \\ $$$$\:\overset{\rightarrow} {{AX}}\:=\:\left({x}−\mathrm{6},\:{y}−\mathrm{2},\:{z}+\mathrm{4}\right) \\ $$$$\:{eq}\:{of}\:{plane}\:\Rightarrow\:\overset{\rightarrow} {{AX}}\:.\:\overset{\rightarrow} {{n}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{60}\left({x}−\mathrm{6}\right)+\mathrm{24}\left({y}−\mathrm{2}\right)+\mathrm{36}\left({z}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}{x}−\mathrm{30}+\mathrm{2}{y}−\mathrm{4}+\mathrm{3}{z}+\mathrm{12}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}{x}+\mathrm{2}{y}+\mathrm{3}{z}−\mathrm{22}=\mathrm{0}\: \\ $$$$ \\ $$
Answered by mr W last updated on 18/Dec/22
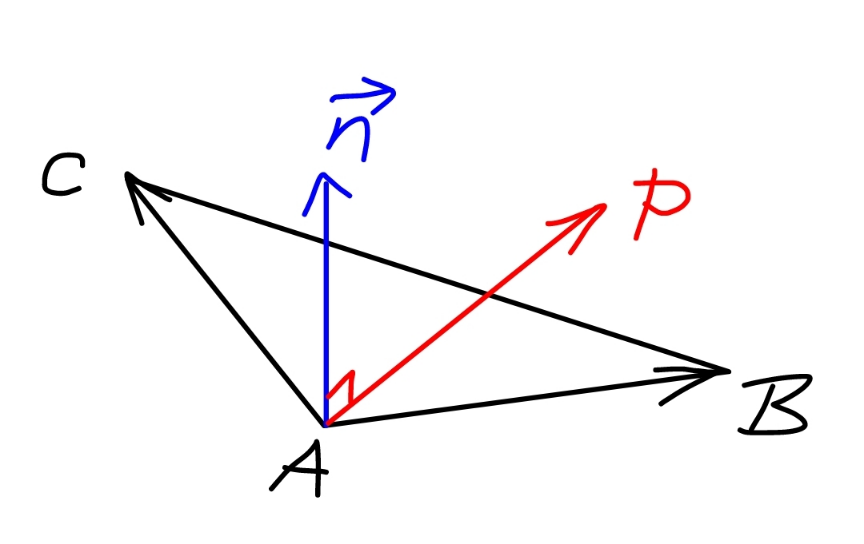
Commented by mr W last updated on 18/Dec/22
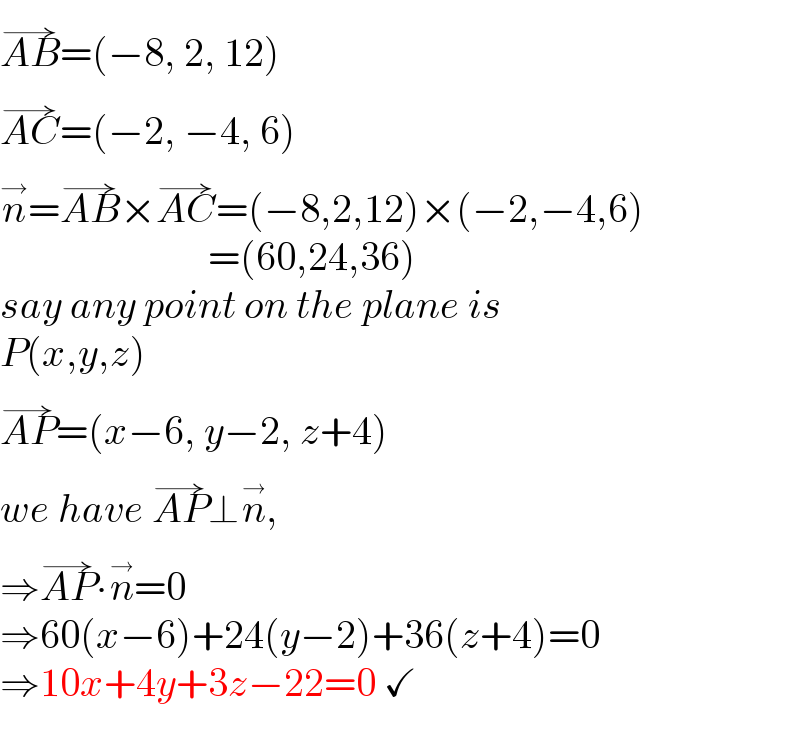
$$\overset{\rightarrow} {{AB}}=\left(−\mathrm{8},\:\mathrm{2},\:\mathrm{12}\right) \\ $$$$\overset{\rightarrow} {{AC}}=\left(−\mathrm{2},\:−\mathrm{4},\:\mathrm{6}\right) \\ $$$$\overset{\rightarrow} {{n}}=\overset{\rightarrow} {{AB}}×\overset{\rightarrow} {{AC}}=\left(−\mathrm{8},\mathrm{2},\mathrm{12}\right)×\left(−\mathrm{2},−\mathrm{4},\mathrm{6}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{60},\mathrm{24},\mathrm{36}\right) \\ $$$${say}\:{any}\:{point}\:{on}\:{the}\:{plane}\:{is} \\ $$$${P}\left({x},{y},{z}\right) \\ $$$$\overset{\rightarrow} {{AP}}=\left({x}−\mathrm{6},\:{y}−\mathrm{2},\:{z}+\mathrm{4}\right) \\ $$$${we}\:{have}\:\overset{\rightarrow} {{AP}}\bot\overset{\rightarrow} {{n}}, \\ $$$$\Rightarrow\overset{\rightarrow} {{AP}}\centerdot\overset{\rightarrow} {{n}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{60}\left({x}−\mathrm{6}\right)+\mathrm{24}\left({y}−\mathrm{2}\right)+\mathrm{36}\left({z}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{10}{x}+\mathrm{4}{y}+\mathrm{3}{z}−\mathrm{22}=\mathrm{0}\:\checkmark \\ $$
Commented by cortano1 last updated on 18/Dec/22

$${why}\:\overset{\rightarrow} {{n}}\:=\:\left(\mathrm{60},\mathrm{24},\mathrm{36}\right)? \\ $$
Commented by mr W last updated on 18/Dec/22
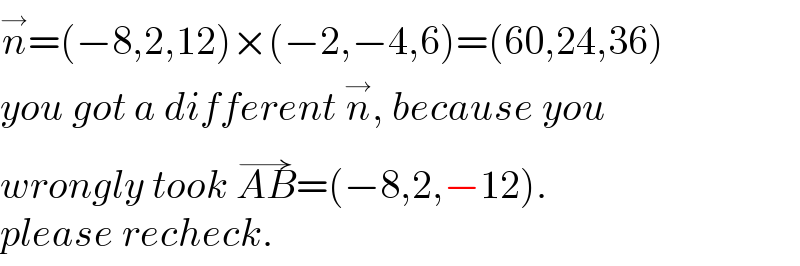
$$\overset{\rightarrow} {{n}}=\left(−\mathrm{8},\mathrm{2},\mathrm{12}\right)×\left(−\mathrm{2},−\mathrm{4},\mathrm{6}\right)=\left(\mathrm{60},\mathrm{24},\mathrm{36}\right) \\ $$$${you}\:{got}\:{a}\:{different}\:\overset{\rightarrow} {{n}},\:{because}\:{you} \\ $$$${wrongly}\:{took}\:\overset{\rightarrow} {{AB}}=\left(−\mathrm{8},\mathrm{2},−\mathrm{12}\right). \\ $$$${please}\:{recheck}. \\ $$
Commented by cortano1 last updated on 18/Dec/22
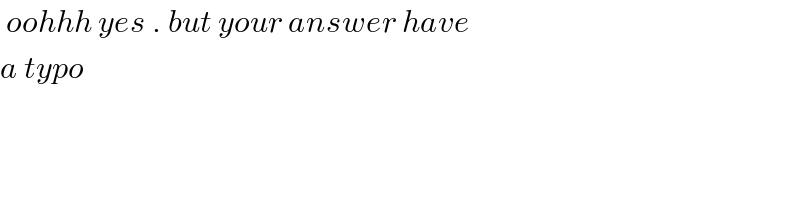
$$\:{oohhh}\:{yes}\:.\:{but}\:{your}\:{answer}\:{have} \\ $$$${a}\:{typo} \\ $$
Commented by mr W last updated on 18/Dec/22
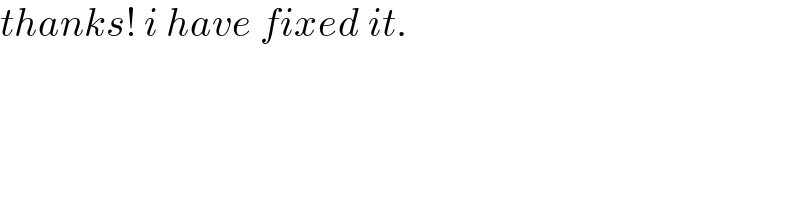
$${thanks}!\:{i}\:{have}\:{fixed}\:{it}. \\ $$
Commented by Mastermind last updated on 18/Dec/22

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{boss} \\ $$
