
Question Number 182940 by mathocean1 last updated on 17/Dec/22
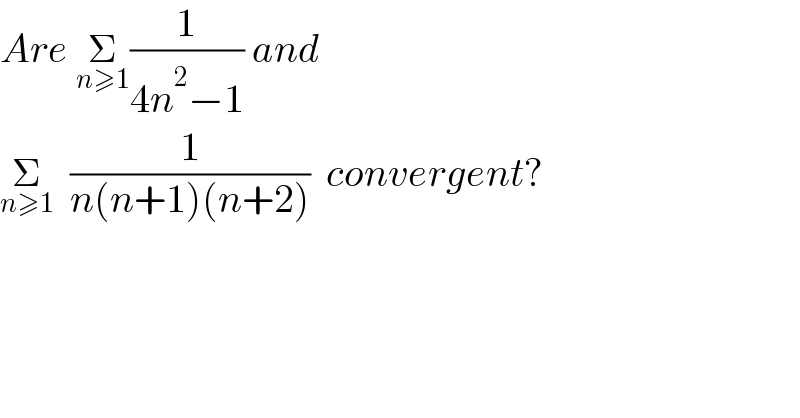
$${Are}\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}\:{and}\: \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:\:{convergent}? \\ $$
Answered by JDamian last updated on 17/Dec/22
![a_n =(1/(4n^2 −1))=(1/((2n−1)(2n+1)))= =(1/2)((1/(2n−1))−(1/(2n+1))) telescoping series S=(1/2)Σ_(k=1) ^∞ ((1/(2n−1))−(1/(2n+1)))= =(1/2)((1/1)−(1/3)+(1/3)−(1/5)+(1/5)−(1/7)+ ...)= =(1/2)[1−lim_(n→∞) ((1/(2n+1)))]=(1/2)](Q182942.png)
$${a}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\:\:\:{telescoping}\:{series} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\:...\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}−\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\right]=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by ARUNG_Brandon_MBU last updated on 17/Dec/22
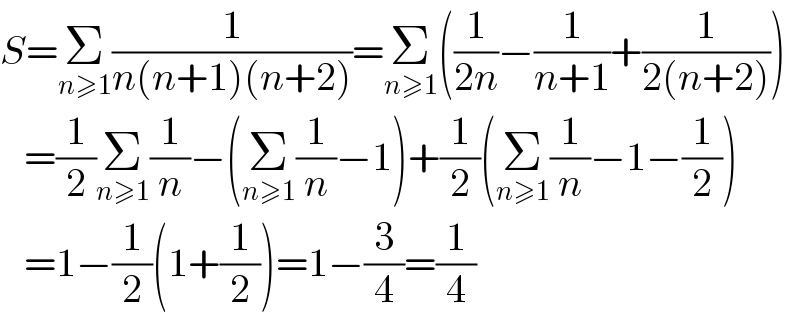
$${S}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}=\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{2}\right)}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}−\left(\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
