
Question Number 182934 by moh777 last updated on 17/Dec/22
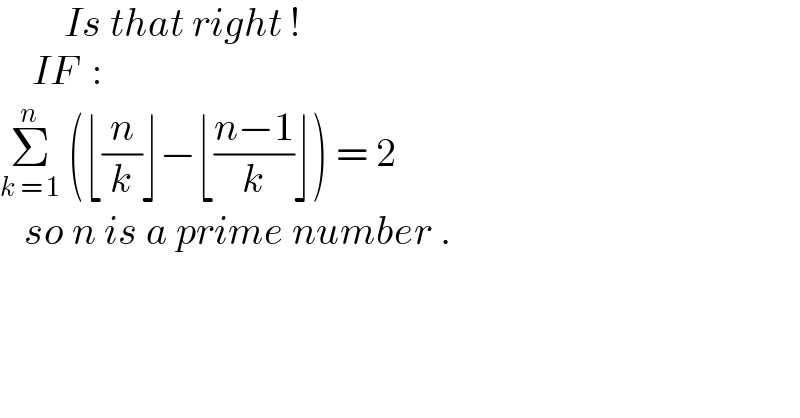
$$\:\:\:\:\:\:\:\:{Is}\:{that}\:{right}\:! \\ $$$$\:\:\:\:{IF}\:\::\: \\ $$$$\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\lfloor\frac{{n}}{{k}}\rfloor−\lfloor\frac{{n}−\mathrm{1}}{{k}}\rfloor\right)\:=\:\mathrm{2} \\ $$$$\:\:\:{so}\:{n}\:{is}\:{a}\:{prime}\:{number}\:. \\ $$
Answered by dre23 last updated on 17/Dec/22
![⇔∀n≥2 Σ_(k=2) ^n ([(n/k)]−[((n−1)/k)])=1 n est premiers n=2 worcks ∀n≥3 ⇔Σ_(k=2) ^(n−1) ([(n/k)]−[((n−1)/k)])=0 f(n,k)=[(n/k)]−[((n−1)/k)] if n is not prime ∃s∈N−{1,n} such n=sp (n/s)=p and((n−1)/s)=p−(1/p), [(n/k)]=p,[((n−1)/k)]=p−1 Σ_(k=2) ^(n−1) ([(n/k)]−[((n−1)/k)])=Σ_(k=2,k≠k) ^(n−1) f(n,k)+p−(p−1)≥p−(p−1)=1 ⇔Σ_(k=2) ^(n−1) f(n,k)≥1>0⇒not true so Σ_(k=1) ^n f(n,k)=2⇒n is prime true](Q182943.png)
$$\Leftrightarrow\forall{n}\geqslant\mathrm{2} \\ $$$$\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\left(\left[\frac{{n}}{{k}}\right]−\left[\frac{{n}−\mathrm{1}}{{k}}\right]\right)=\mathrm{1}\:{n}\:{est}\:{premiers} \\ $$$${n}=\mathrm{2}\:{worcks}\:\forall{n}\geqslant\mathrm{3} \\ $$$$\Leftrightarrow\underset{{k}=\mathrm{2}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\left[\frac{{n}}{{k}}\right]−\left[\frac{{n}−\mathrm{1}}{{k}}\right]\right)=\mathrm{0} \\ $$$${f}\left({n},{k}\right)=\left[\frac{{n}}{{k}}\right]−\left[\frac{{n}−\mathrm{1}}{{k}}\right] \\ $$$${if}\:{n}\:{is}\:{not}\:{prime}\:\exists{s}\in\mathbb{N}−\left\{\mathrm{1},{n}\right\}\:{such}\:{n}={sp} \\ $$$$\frac{{n}}{{s}}={p}\:{and}\frac{{n}−\mathrm{1}}{{s}}={p}−\frac{\mathrm{1}}{{p}}, \\ $$$$\left[\frac{{n}}{{k}}\right]={p},\left[\frac{{n}−\mathrm{1}}{{k}}\right]={p}−\mathrm{1} \\ $$$$\underset{{k}=\mathrm{2}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\left[\frac{{n}}{{k}}\right]−\left[\frac{{n}−\mathrm{1}}{{k}}\right]\right)=\underset{{k}=\mathrm{2},{k}\neq{k}} {\overset{{n}−\mathrm{1}} {\sum}}{f}\left({n},{k}\right)+{p}−\left({p}−\mathrm{1}\right)\geqslant{p}−\left({p}−\mathrm{1}\right)=\mathrm{1} \\ $$$$\Leftrightarrow\underset{{k}=\mathrm{2}} {\overset{{n}−\mathrm{1}} {\sum}}{f}\left({n},{k}\right)\geqslant\mathrm{1}>\mathrm{0}\Rightarrow{not}\:{true} \\ $$$${so}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left({n},{k}\right)=\mathrm{2}\Rightarrow{n}\:{is}\:{prime}\:{true} \\ $$$$ \\ $$$$ \\ $$
