
Question Number 182848 by malithxd last updated on 15/Dec/22
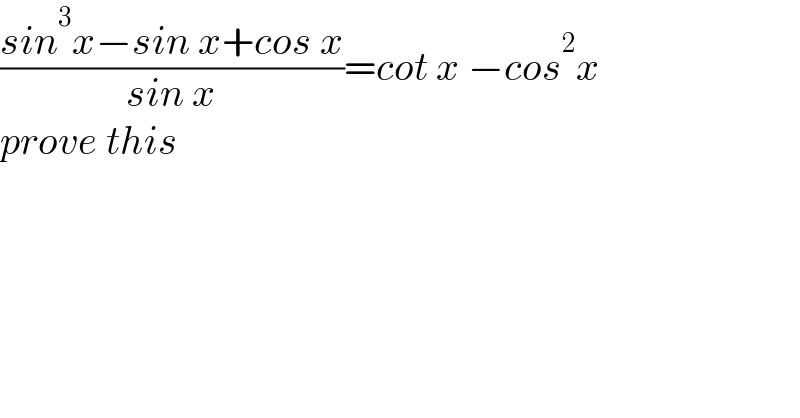
$$\frac{{sin}^{\mathrm{3}} {x}−{sin}\:{x}+{cos}\:{x}}{{sin}\:{x}}={cot}\:{x}\:−{cos}^{\mathrm{2}} {x} \\ $$$${prove}\:{this} \\ $$$$ \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 15/Dec/22
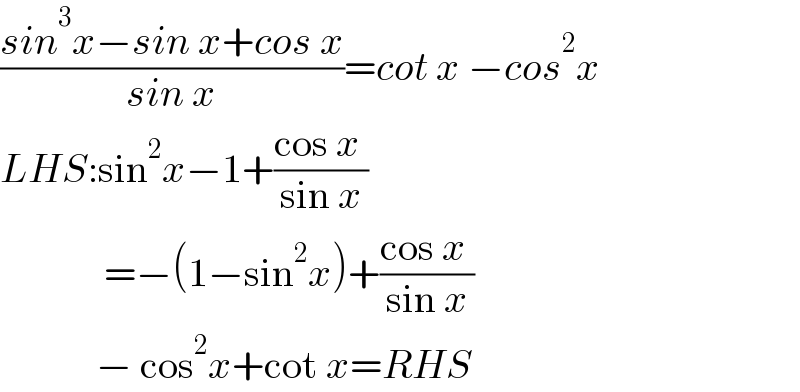
$$\frac{{sin}^{\mathrm{3}} {x}−{sin}\:{x}+{cos}\:{x}}{{sin}\:{x}}={cot}\:{x}\:−{cos}^{\mathrm{2}} {x} \\ $$$${LHS}:\mathrm{sin}^{\mathrm{2}} {x}−\mathrm{1}+\frac{\mathrm{cos}\:{x}\:}{\mathrm{sin}\:{x}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=−\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}\right)+\frac{\mathrm{cos}\:{x}\:}{\mathrm{sin}\:{x}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\:\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{cot}\:{x}={RHS}\: \\ $$
Answered by manxsol last updated on 15/Dec/22
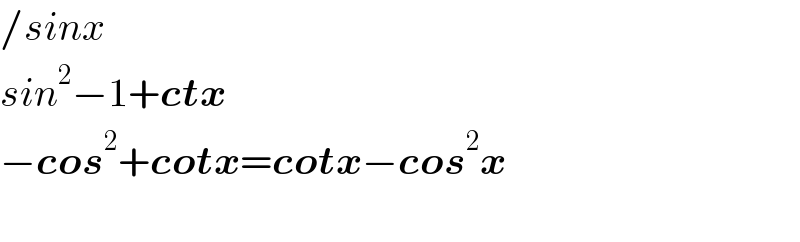
$$/{sinx} \\ $$$${sin}^{\mathrm{2}} −\mathrm{1}+\boldsymbol{{ctx}} \\ $$$$−\boldsymbol{{cos}}^{\mathrm{2}} +\boldsymbol{{cotx}}=\boldsymbol{{cotx}}−\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{x}} \\ $$$$ \\ $$
Answered by cortano1 last updated on 15/Dec/22
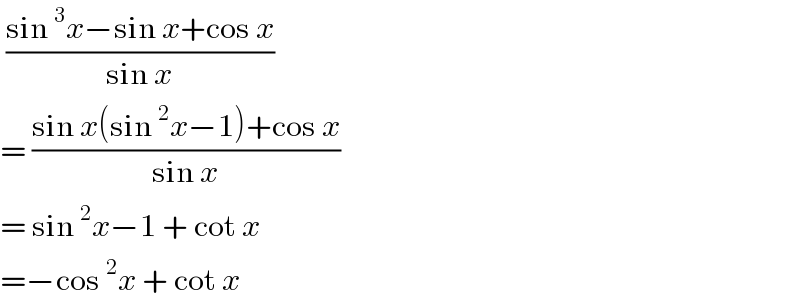
$$\:\frac{\mathrm{sin}\:^{\mathrm{3}} {x}−\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}\: \\ $$$$=\:\frac{\mathrm{sin}\:{x}\left(\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{1}\right)+\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}} \\ $$$$=\:\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{1}\:+\:\mathrm{cot}\:{x} \\ $$$$=−\mathrm{cos}\:^{\mathrm{2}} {x}\:+\:\mathrm{cot}\:{x}\: \\ $$
