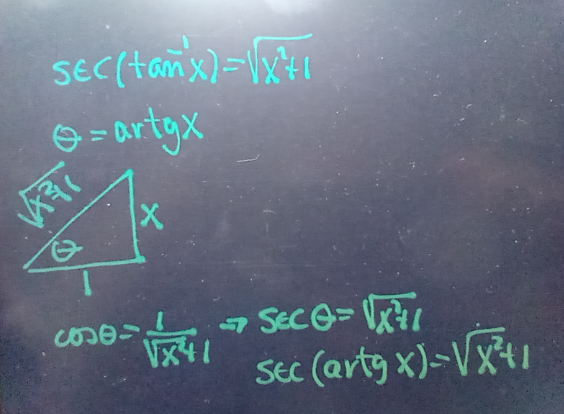Question Number 182842 by malwan last updated on 15/Dec/22
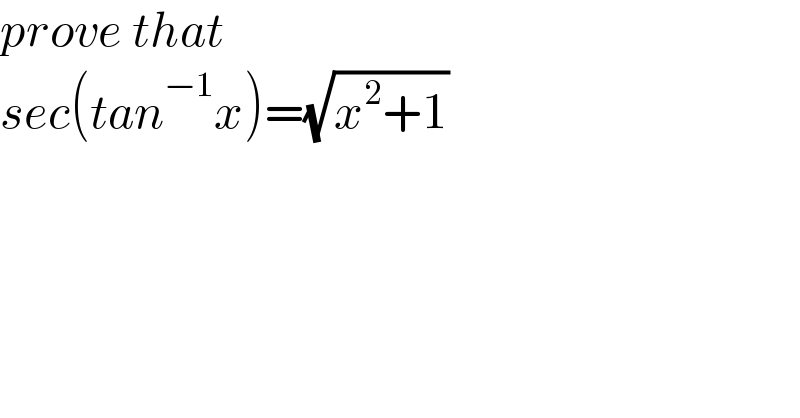
$${prove}\:{that} \\ $$$${sec}\left({tan}^{−\mathrm{1}} {x}\right)=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$
Answered by cortano1 last updated on 15/Dec/22
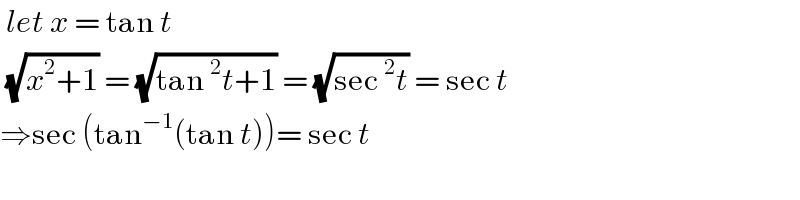
$$\:{let}\:{x}\:=\:\mathrm{tan}\:{t}\: \\ $$$$\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:=\:\sqrt{\mathrm{tan}\:^{\mathrm{2}} {t}+\mathrm{1}}\:=\:\sqrt{\mathrm{sec}\:^{\mathrm{2}} {t}}\:=\:\mathrm{sec}\:{t} \\ $$$$\Rightarrow\mathrm{sec}\:\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:{t}\right)\right)=\:\mathrm{sec}\:{t}\: \\ $$
Commented by malwan last updated on 15/Dec/22

$${thank}\:{you}\:{sir} \\ $$
Answered by BaliramKumar last updated on 15/Dec/22
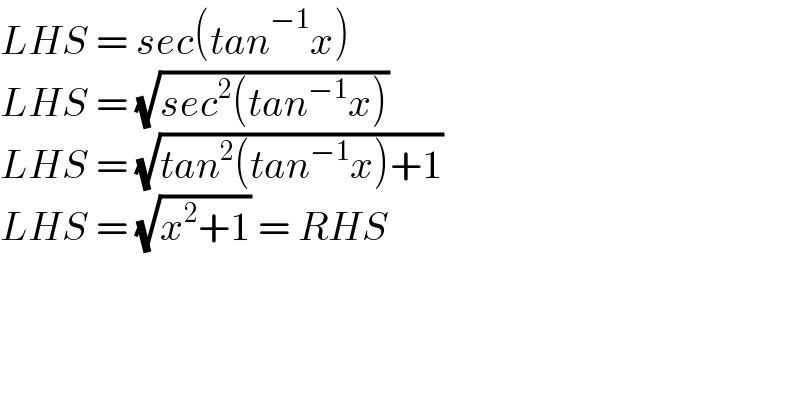
$${LHS}\:=\:{sec}\left({tan}^{−\mathrm{1}} {x}\right) \\ $$$${LHS}\:=\:\sqrt{{sec}^{\mathrm{2}} \left({tan}^{−\mathrm{1}} {x}\right)} \\ $$$${LHS}\:=\:\sqrt{{tan}^{\mathrm{2}} \left({tan}^{−\mathrm{1}} {x}\right)+\mathrm{1}} \\ $$$${LHS}\:=\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:=\:{RHS} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by malwan last updated on 15/Dec/22
$${thank}\:{you}\:{so}\:{much} \\ $$
Answered by manxsol last updated on 16/Dec/22