
Question Number 18284 by tawa tawa last updated on 18/Jul/17

$$\mathrm{If}\:\mathrm{k}\:\mathrm{is}\:\mathrm{any}\:\mathrm{possible}\:\mathrm{number}.\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{size}\:\mathrm{of}\:\mathrm{angle}\:\mathrm{between}\:\mathrm{the}\:\mathrm{vectors} \\ $$$$\mathrm{a}\left(\mathrm{K},\:\mathrm{k}\right)\:\mathrm{and}\:\mathrm{b}\left(−\:\mathrm{3},\:\mathrm{4}\right) \\ $$
Answered by Arnab Maiti last updated on 18/Jul/17
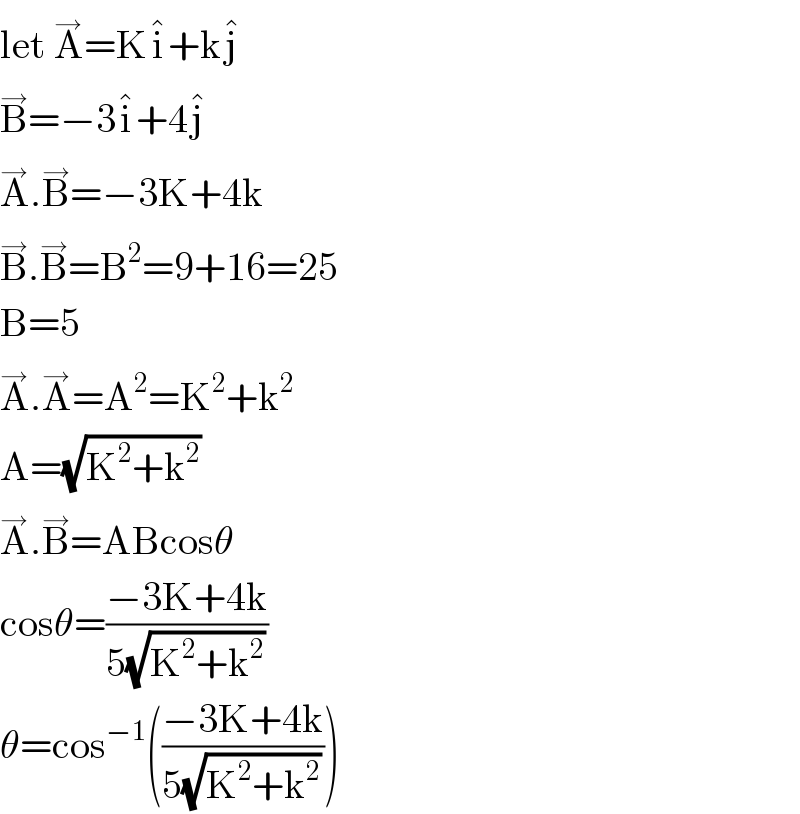
$$\mathrm{let}\:\overset{\rightarrow} {\mathrm{A}}=\mathrm{K}\hat {\mathrm{i}}+\mathrm{k}\hat {\mathrm{j}} \\ $$$$\overset{\rightarrow} {\mathrm{B}}=−\mathrm{3}\hat {\mathrm{i}}+\mathrm{4}\hat {\mathrm{j}} \\ $$$$\overset{\rightarrow} {\mathrm{A}}.\overset{\rightarrow} {\mathrm{B}}=−\mathrm{3K}+\mathrm{4k} \\ $$$$\overset{\rightarrow} {\mathrm{B}}.\overset{\rightarrow} {\mathrm{B}}=\mathrm{B}^{\mathrm{2}} =\mathrm{9}+\mathrm{16}=\mathrm{25} \\ $$$$\mathrm{B}=\mathrm{5} \\ $$$$\overset{\rightarrow} {\mathrm{A}}.\overset{\rightarrow} {\mathrm{A}}=\mathrm{A}^{\mathrm{2}} =\mathrm{K}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} \\ $$$$\mathrm{A}=\sqrt{\mathrm{K}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} } \\ $$$$\overset{\rightarrow} {\mathrm{A}}.\overset{\rightarrow} {\mathrm{B}}=\mathrm{ABcos}\theta \\ $$$$\mathrm{cos}\theta=\frac{−\mathrm{3K}+\mathrm{4k}}{\mathrm{5}\sqrt{\mathrm{K}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} }} \\ $$$$\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{−\mathrm{3K}+\mathrm{4k}}{\mathrm{5}\sqrt{\mathrm{K}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} }}\right) \\ $$
Commented by tawa tawa last updated on 18/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
