
Question Number 182836 by mathlove last updated on 15/Dec/22

Answered by floor(10²Eta[1]) last updated on 15/Dec/22
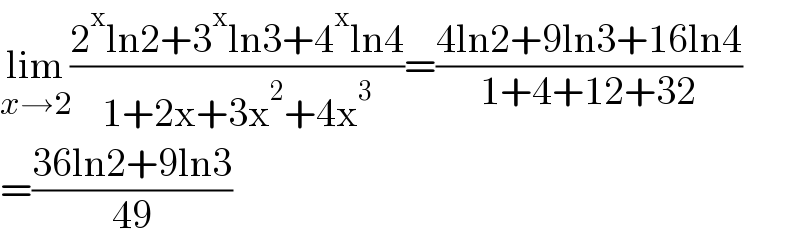
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{2}^{\mathrm{x}} \mathrm{ln2}+\mathrm{3}^{\mathrm{x}} \mathrm{ln3}+\mathrm{4}^{\mathrm{x}} \mathrm{ln4}}{\mathrm{1}+\mathrm{2x}+\mathrm{3x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{3}} }=\frac{\mathrm{4ln2}+\mathrm{9ln3}+\mathrm{16ln4}}{\mathrm{1}+\mathrm{4}+\mathrm{12}+\mathrm{32}} \\ $$$$=\frac{\mathrm{36ln2}+\mathrm{9ln3}}{\mathrm{49}} \\ $$
Commented by mathlove last updated on 17/Dec/22
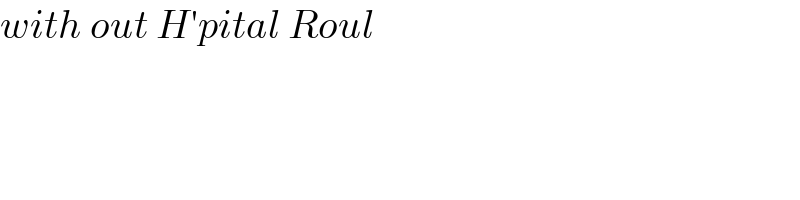
$${with}\:{out}\:{H}'{pital}\:{Roul} \\ $$
Answered by manolex last updated on 15/Dec/22
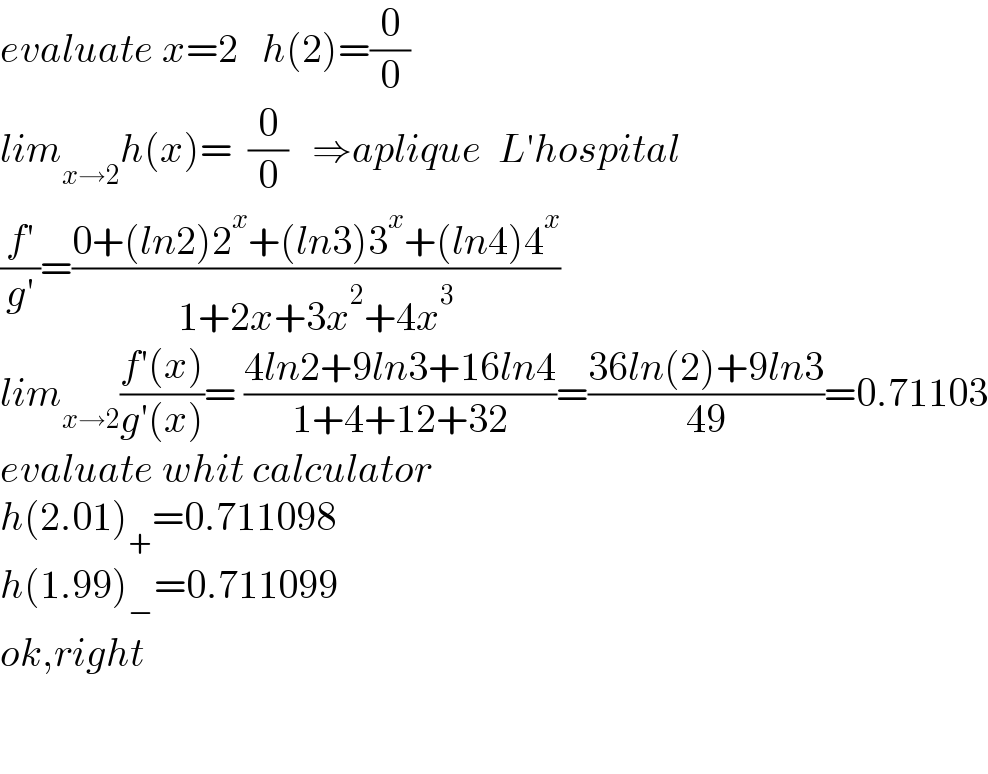
$${evaluate}\:{x}=\mathrm{2}\:\:\:{h}\left(\mathrm{2}\right)=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$${lim}_{{x}\rightarrow\mathrm{2}} {h}\left({x}\right)=\:\:\frac{\mathrm{0}}{\mathrm{0}}\:\:\:\Rightarrow{aplique}\:\:{L}'{hospital} \\ $$$$\frac{{f}'}{{g}'}=\frac{\mathrm{0}+\left({ln}\mathrm{2}\right)\mathrm{2}^{{x}} +\left({ln}\mathrm{3}\right)\mathrm{3}^{{x}} +\left({ln}\mathrm{4}\right)\mathrm{4}^{{x}} }{\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} } \\ $$$${lim}_{{x}\rightarrow\mathrm{2}} \frac{{f}'\left({x}\right)}{{g}'\left({x}\right)}=\:\frac{\mathrm{4}{ln}\mathrm{2}+\mathrm{9}{ln}\mathrm{3}+\mathrm{16}{ln}\mathrm{4}}{\mathrm{1}+\mathrm{4}+\mathrm{12}+\mathrm{32}}=\frac{\mathrm{36}{ln}\left(\mathrm{2}\right)+\mathrm{9}{ln}\mathrm{3}}{\mathrm{49}}=\mathrm{0}.\mathrm{71103} \\ $$$${evaluate}\:{whit}\:{calculator} \\ $$$${h}\left(\mathrm{2}.\mathrm{01}\right)_{+} =\mathrm{0}.\mathrm{711098} \\ $$$${h}\left(\mathrm{1}.\mathrm{99}\right)_{−} =\mathrm{0}.\mathrm{711099} \\ $$$${ok},{right} \\ $$$$ \\ $$$$ \\ $$
