
Question Number 182810 by Mastermind last updated on 14/Dec/22
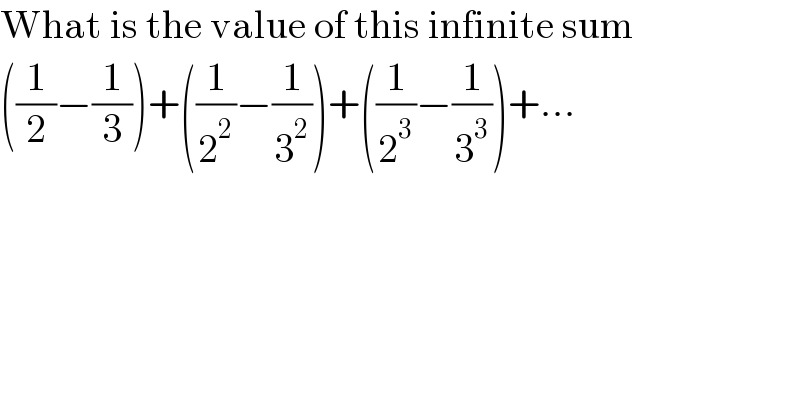
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{infinite}\:\mathrm{sum} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\right)+\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\right)+... \\ $$$$ \\ $$$$ \\ $$
Answered by JDamian last updated on 14/Dec/22
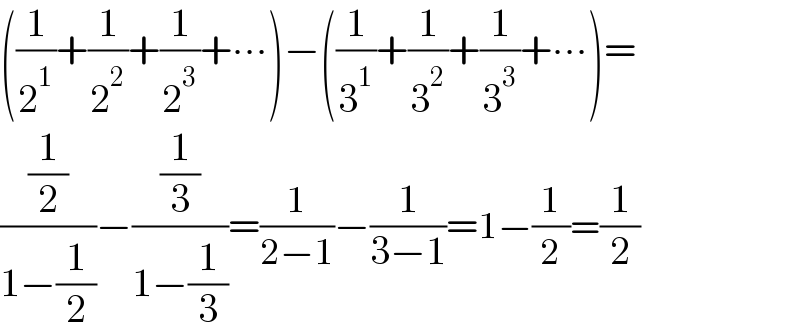
$$\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+\centerdot\centerdot\centerdot\right)−\left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+\centerdot\centerdot\centerdot\right)= \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}−\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}=\frac{\mathrm{1}}{\mathrm{2}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}−\mathrm{1}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by HeferH last updated on 14/Dec/22
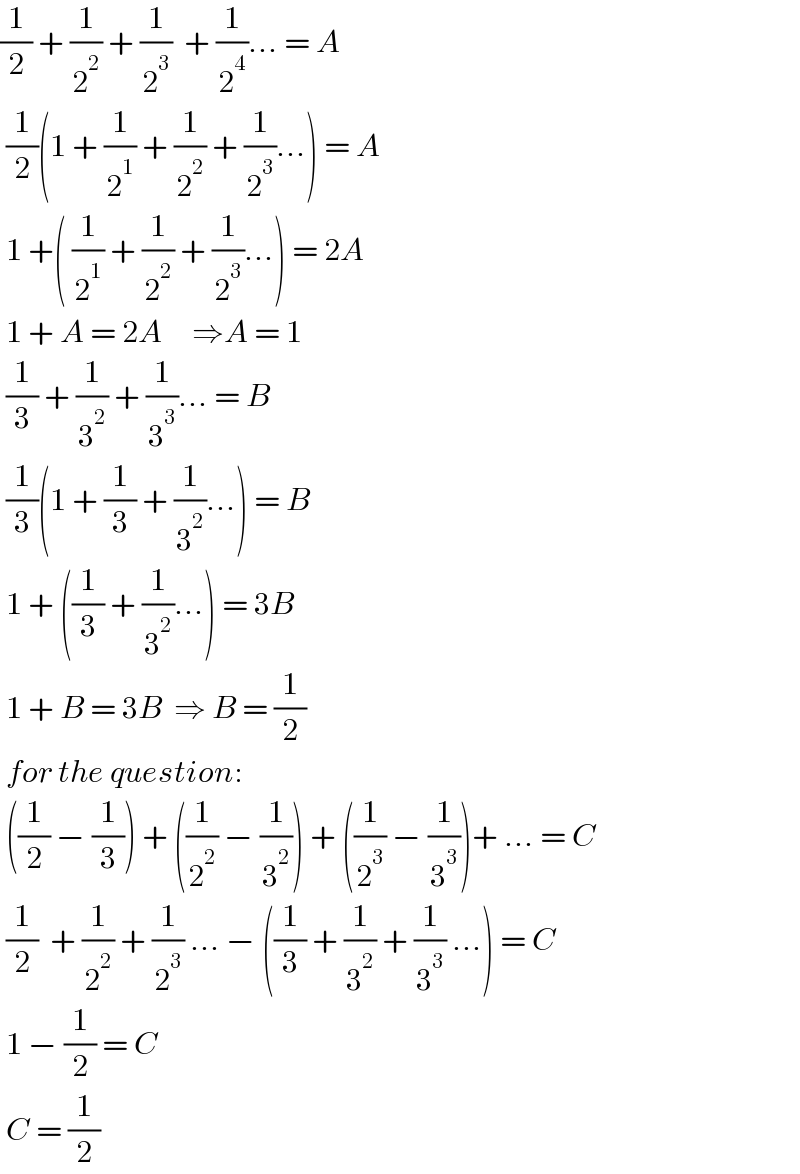
$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\:\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }...\:=\:{A} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }...\right)\:=\:{A} \\ $$$$\:\mathrm{1}\:+\left(\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }...\right)\:=\:\mathrm{2}{A} \\ $$$$\:\mathrm{1}\:+\:{A}\:=\:\mathrm{2}{A}\:\:\:\:\:\Rightarrow{A}\:=\:\mathrm{1} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }...\:=\:{B} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }...\right)\:=\:{B} \\ $$$$\:\mathrm{1}\:+\:\left(\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }...\right)\:=\:\mathrm{3}{B} \\ $$$$\:\mathrm{1}\:+\:{B}\:=\:\mathrm{3}{B}\:\:\Rightarrow\:{B}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:{for}\:{the}\:{question}: \\ $$$$\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\right)\:+\:\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\right)\:+\:\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\:−\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\right)+\:...\:=\:{C} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\:\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\:...\:−\:\left(\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\:...\right)\:=\:{C} \\ $$$$\:\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:{C} \\ $$$$\:{C}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
