
Question Number 182804 by mnjuly1970 last updated on 14/Dec/22
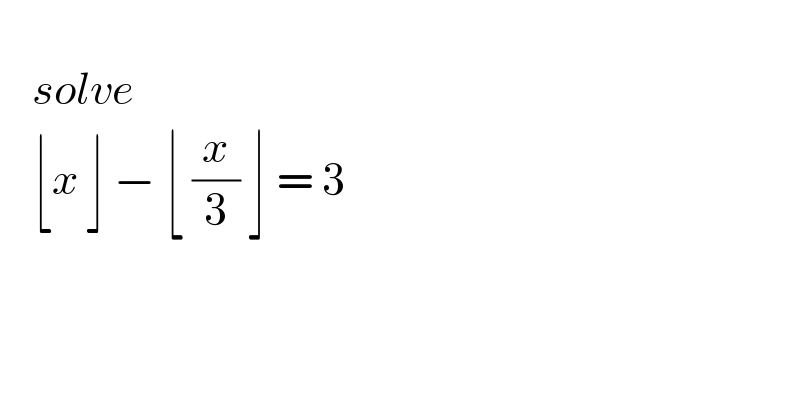
$$ \\ $$$$\:\:\:\:{solve} \\ $$$$\:\:\:\:\lfloor\underset{} {\overset{} {{x}}}\:\rfloor\:−\:\lfloor\:\frac{{x}}{\mathrm{3}}\:\rfloor\:=\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\: \\ $$
Answered by mahdipoor last updated on 14/Dec/22
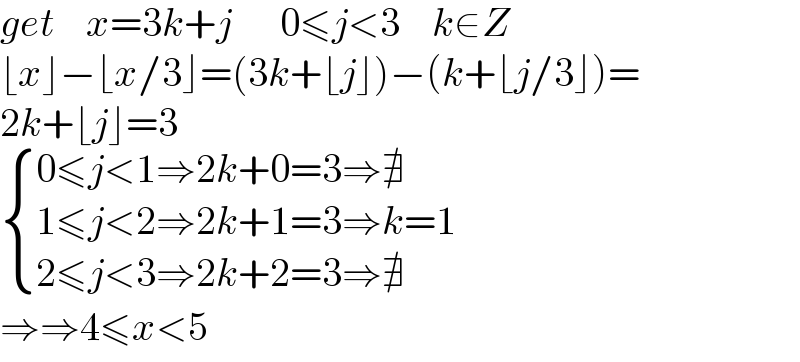
$${get}\:\:\:\:{x}=\mathrm{3}{k}+{j}\:\:\:\:\:\:\mathrm{0}\leqslant{j}<\mathrm{3}\:\:\:\:{k}\in{Z} \\ $$$$\lfloor{x}\rfloor−\lfloor{x}/\mathrm{3}\rfloor=\left(\mathrm{3}{k}+\lfloor{j}\rfloor\right)−\left({k}+\lfloor{j}/\mathrm{3}\rfloor\right)= \\ $$$$\mathrm{2}{k}+\lfloor{j}\rfloor=\mathrm{3} \\ $$$$\begin{cases}{\mathrm{0}\leqslant{j}<\mathrm{1}\Rightarrow\mathrm{2}{k}+\mathrm{0}=\mathrm{3}\Rightarrow\nexists}\\{\mathrm{1}\leqslant{j}<\mathrm{2}\Rightarrow\mathrm{2}{k}+\mathrm{1}=\mathrm{3}\Rightarrow{k}=\mathrm{1}}\\{\mathrm{2}\leqslant{j}<\mathrm{3}\Rightarrow\mathrm{2}{k}+\mathrm{2}=\mathrm{3}\Rightarrow\nexists}\end{cases} \\ $$$$\Rightarrow\Rightarrow\mathrm{4}\leqslant{x}<\mathrm{5} \\ $$
Commented by mnjuly1970 last updated on 14/Dec/22
$$\:{very}\:{nice}\:{sir}\:{mahdipoor} \\ $$
Answered by mr W last updated on 14/Dec/22
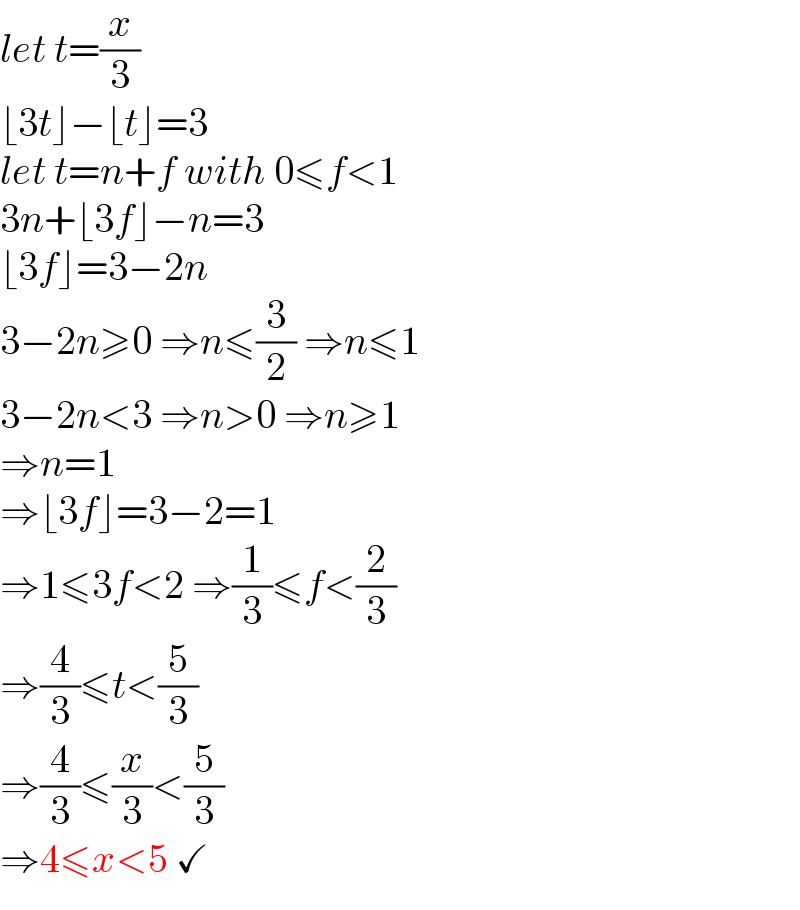
$${let}\:{t}=\frac{{x}}{\mathrm{3}} \\ $$$$\lfloor\mathrm{3}{t}\rfloor−\lfloor{t}\rfloor=\mathrm{3} \\ $$$${let}\:{t}={n}+{f}\:{with}\:\mathrm{0}\leqslant{f}<\mathrm{1} \\ $$$$\mathrm{3}{n}+\lfloor\mathrm{3}{f}\rfloor−{n}=\mathrm{3} \\ $$$$\lfloor\mathrm{3}{f}\rfloor=\mathrm{3}−\mathrm{2}{n} \\ $$$$\mathrm{3}−\mathrm{2}{n}\geqslant\mathrm{0}\:\Rightarrow{n}\leqslant\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow{n}\leqslant\mathrm{1} \\ $$$$\mathrm{3}−\mathrm{2}{n}<\mathrm{3}\:\Rightarrow{n}>\mathrm{0}\:\Rightarrow{n}\geqslant\mathrm{1} \\ $$$$\Rightarrow{n}=\mathrm{1} \\ $$$$\Rightarrow\lfloor\mathrm{3}{f}\rfloor=\mathrm{3}−\mathrm{2}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}\leqslant\mathrm{3}{f}<\mathrm{2}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{3}}\leqslant{f}<\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{4}}{\mathrm{3}}\leqslant{t}<\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{4}}{\mathrm{3}}\leqslant\frac{{x}}{\mathrm{3}}<\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{4}\leqslant{x}<\mathrm{5}\:\checkmark \\ $$
Commented by mnjuly1970 last updated on 14/Dec/22
$${thx}\:{sir}\:{W}\:{very}\:{nice}\:{solution} \\ $$
