
Question Number 182791 by Matica last updated on 14/Dec/22
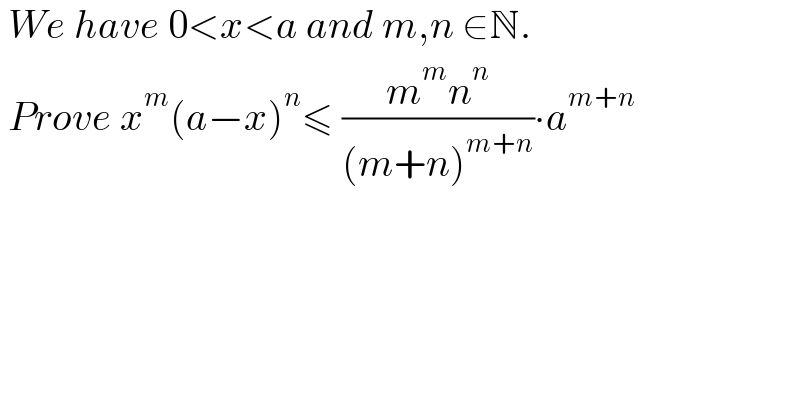
$$\:{We}\:{have}\:\mathrm{0}<{x}<{a}\:{and}\:{m},{n}\:\in\mathbb{N}. \\ $$ $$\:{Prove}\:{x}^{{m}} \left({a}−{x}\right)^{{n}} \leqslant\:\frac{{m}^{{m}} {n}^{{n}} }{\left({m}+{n}\right)^{{m}+{n}} }\centerdot{a}^{{m}+{n}} \\ $$
Answered by mahdipoor last updated on 14/Dec/22
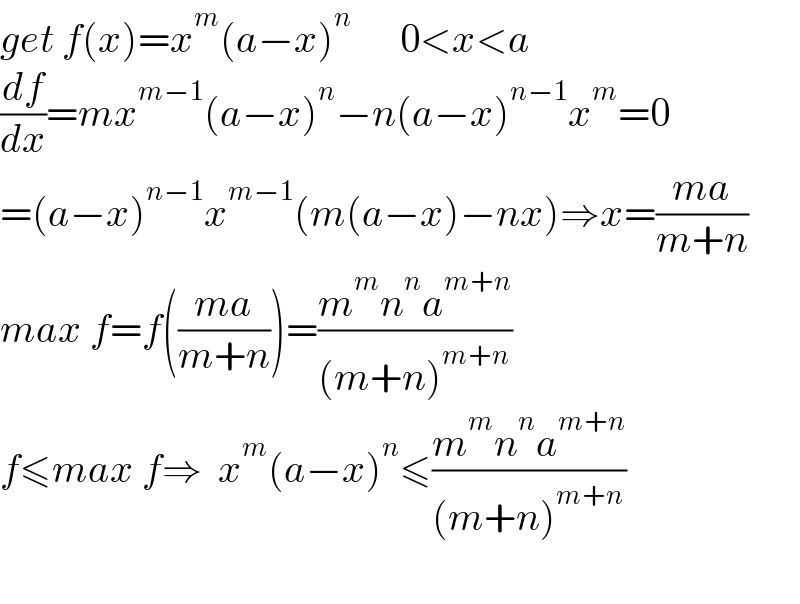
$${get}\:{f}\left({x}\right)={x}^{{m}} \left({a}−{x}\right)^{{n}} \:\:\:\:\:\:\mathrm{0}<{x}<{a} \\ $$ $$\frac{{df}}{{dx}}={mx}^{{m}−\mathrm{1}} \left({a}−{x}\right)^{{n}} −{n}\left({a}−{x}\right)^{{n}−\mathrm{1}} {x}^{{m}} =\mathrm{0} \\ $$ $$=\left({a}−{x}\right)^{{n}−\mathrm{1}} {x}^{{m}−\mathrm{1}} \left({m}\left({a}−{x}\right)−{nx}\right)\Rightarrow{x}=\frac{{ma}}{{m}+{n}} \\ $$ $${max}\:{f}={f}\left(\frac{{ma}}{{m}+{n}}\right)=\frac{{m}^{{m}} {n}^{{n}} {a}^{{m}+{n}} }{\left({m}+{n}\right)^{{m}+{n}} } \\ $$ $${f}\leqslant{max}\:{f}\Rightarrow\:\:{x}^{{m}} \left({a}−{x}\right)^{{n}} \leqslant\frac{{m}^{{m}} {n}^{{n}} {a}^{{m}+{n}} }{\left({m}+{n}\right)^{{m}+{n}} } \\ $$ $$ \\ $$
Commented byMatica last updated on 15/Dec/22

$${thank}\:{you}\:\:{a}\:{lot} \\ $$
Answered by dre23 last updated on 15/Dec/22
![x^m (1−x)^n ≤((m^m n^n )/((m+n)^(m+n) )),....S by x→ax⇔∀ 0<x<1 .....S ⇔((x/m))^m (((1−x)/n))^n ≤(1/((n+m)^(n+m) ))⇔S mln((x/m))+nln(((1−x)/n))....S x→^f ln(x) is concave,f′′=−(1/x^2 )<0,∀x∈]0,1] (m/(n+m))ln((x/m))+(n/(n+m))ln(((1−x)/n))≤ln((1/(n+m))) (n+m){(m/(m+n))ln((x/m))+(n/(n+m))ln(((1−x)/n))}≤ (n+m)ln((x/(n+m))+((1−x)/(n+m)))≤(n+m)ln((1/(n+m)))=ln((1/((n+m)^(n+m) ))) ⇔s≤ln((1/((n+m)^(n+m) ))) tack e ⇔((x/m))^m (((1−x)/n))^n ≤((1/(n+m)))^(n+m) ..True](Q182844.png)
$${x}^{{m}} \left(\mathrm{1}−{x}\right)^{{n}} \leqslant\frac{{m}^{{m}} {n}^{{n}} }{\left({m}+{n}\right)^{{m}+{n}} },....{S} \\ $$ $${by}\:{x}\rightarrow{ax}\Leftrightarrow\forall\:\mathrm{0}<{x}<\mathrm{1}\:.....{S} \\ $$ $$\Leftrightarrow\left(\frac{{x}}{{m}}\right)^{{m}} \left(\frac{\mathrm{1}−{x}}{{n}}\right)^{{n}} \leqslant\frac{\mathrm{1}}{\left({n}+{m}\right)^{{n}+{m}} }\Leftrightarrow{S} \\ $$ $${mln}\left(\frac{{x}}{{m}}\right)+{nln}\left(\frac{\mathrm{1}−{x}}{{n}}\right)....{S} \\ $$ $$\left.{x}\left.\overset{{f}} {\rightarrow}{ln}\left({x}\right)\:{is}\:{concave},{f}''=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }<\mathrm{0},\forall{x}\in\right]\mathrm{0},\mathrm{1}\right] \\ $$ $$\frac{{m}}{{n}+{m}}{ln}\left(\frac{{x}}{{m}}\right)+\frac{{n}}{{n}+{m}}{ln}\left(\frac{\mathrm{1}−{x}}{{n}}\right)\leqslant{ln}\left(\frac{\mathrm{1}}{{n}+{m}}\right) \\ $$ $$\left({n}+{m}\right)\left\{\frac{{m}}{{m}+{n}}{ln}\left(\frac{{x}}{{m}}\right)+\frac{{n}}{{n}+{m}}{ln}\left(\frac{\mathrm{1}−{x}}{{n}}\right)\right\}\leqslant \\ $$ $$\left({n}+{m}\right){ln}\left(\frac{{x}}{{n}+{m}}+\frac{\mathrm{1}−{x}}{{n}+{m}}\right)\leqslant\left({n}+{m}\right){ln}\left(\frac{\mathrm{1}}{{n}+{m}}\right)={ln}\left(\frac{\mathrm{1}}{\left({n}+{m}\right)^{{n}+{m}} }\right) \\ $$ $$\Leftrightarrow{s}\leqslant{ln}\left(\frac{\mathrm{1}}{\left({n}+{m}\right)^{{n}+{m}} }\right)\:{tack}\:{e} \\ $$ $$\Leftrightarrow\left(\frac{{x}}{{m}}\right)^{{m}} \left(\frac{\mathrm{1}−{x}}{{n}}\right)^{{n}} \leqslant\left(\frac{\mathrm{1}}{{n}+{m}}\right)^{{n}+{m}} ..{True} \\ $$ $$ \\ $$ $$ \\ $$ $$ \\ $$ $$ \\ $$ $$ \\ $$
